如图,已知在侧棱垂直于底面的三棱柱 中,
中,
 ,且
,且 ,点
,点 是
是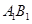 中点.
中点.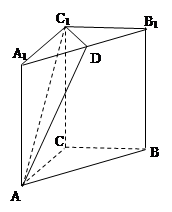
(1)求证:平面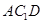 ⊥平面
⊥平面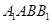 ;
;
(2)若直线 与平面
与平面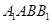 所成角的正弦值为
所成角的正弦值为 ,
,
求三棱锥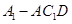 的体积.
的体积.
某高校从今年参加自主招生考试的学生中随机抽取容量为 的学生成绩样本,得到频率分布表如下:
的学生成绩样本,得到频率分布表如下:
| 组数 |
分组 |
频数 |
频率 |
| 第一组 |
[230,235) |
8 |
0.16 |
| 第二组 |
[235,240) |
 |
0.24 |
| 第三组 |
[240,245) |
15 |
 |
| 第四组 |
[245,250) |
10 |
0.20 |
| 第五组 |
[250,255] |
5 |
0.10 |
| 合计 |
 |
1.00 |
(1)求 的值;
的值;
(2)为了选拔出更加优秀的学生,该高校决定在第三、四、五组中用分层抽样的方法抽取6名学生进行第二轮考核,分别求第三、四、五组参加考核的人数;
(3)在(2)的前提下,高校决定从这6名学生中择优录取2名学生,求2人中至少有1人是第四组的概率.
设函数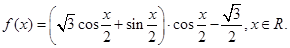
(1)求函数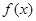 的最小正周期;
的最小正周期;
(2)记 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为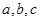 ,若
,若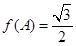 且
且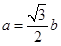 ,求角B的值.
,求角B的值.
已知函数 的图象在
的图象在 上连续,定义:
上连续,定义: ,
, .其中,
.其中, 表示函数
表示函数 在
在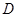 上的最小值,
上的最小值,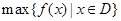 表示函数
表示函数 在
在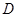 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数 ,使得
,使得 对任意的
对任意的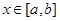 成立,则称函数
成立,则称函数 为
为 上的“
上的“ 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若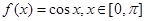 ,试写出
,试写出 ,
, 的表达式;
的表达式;
(Ⅱ)已知函数 ,试判断
,试判断 是否为
是否为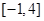 上的“
上的“ 阶收缩函数”.如果是,求出对应的
阶收缩函数”.如果是,求出对应的 ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知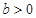 ,函数
,函数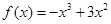 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.
已知函数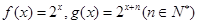 ,点
,点 、
、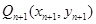 在函数
在函数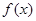 的图象上,
的图象上,
点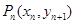 在函数
在函数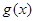 的图象上,设
的图象上,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和为
项和为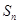 ;
;
(3)已知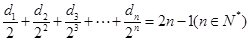 ,记数列
,记数列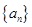 的前
的前 项和为
项和为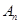 ,数列
,数列 的前
的前 项和为
项和为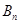 ,试比较
,试比较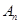 与
与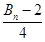 的大小.
的大小.