已知 ,
,
⑴判断 的奇偶性; ⑵证明
的奇偶性; ⑵证明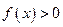 .
.
已知函数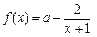 .
.
(1)当a = 4,解不等式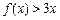 ;
;
(2)若函数 是奇函数,求a的值;
是奇函数,求a的值;
(3)若不等式 在
在 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
(本小题满分13分)
已知数列 满足:
满足: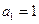 ,
,
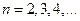
(I)求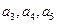 得值;
得值;
(II)设 求证:数列
求证:数列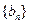 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III)对任意的 ,在数列
,在数列 中是否存在连续的
中是否存在连续的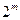 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这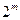 项,并证明这
项,并证明这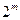 项构成等差数列;若不存在,说明理由。
项构成等差数列;若不存在,说明理由。
(本小题满分13分)
已知椭圆C的对称中心为原点O,焦点在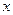 轴上,离心率为
轴上,离心率为 ,且点
,且点 在该椭圆上。
在该椭圆上。
(I)求椭圆C的方程;
(II)过椭圆C的左焦点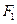 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 的面积为
的面积为 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。
(本小题满分14分)
已知函数 与函数
与函数 。
。
(I)若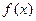 ,
, 的图像在点
的图像在点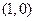 处有公共的切线,求实数
处有公共的切线,求实数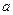 的值;
的值;
(II)设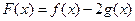 ,求函数
,求函数 的值。
的值。
(本小题满分14分)
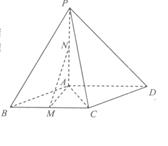
如图:在四棱锥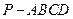 中,底面ABCD是菱形,
中,底面ABCD是菱形,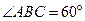 ,
,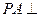 平面ABCD,点M,N分别为BC,PA的中点,且
平面ABCD,点M,N分别为BC,PA的中点,且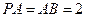
(I)证明: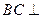 平面AMN;
平面AMN;
(II)求三棱锥N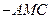 的体积;
的体积;
(III)在线段PD上是否存在一点E,使得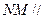 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。