在平面直角坐标系 中,抛物线 的顶点在原点,经过点 ,其焦点 在 轴上.
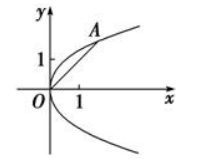
(1)求抛物线
的标准方程;
(2)求过点
,且与直线
垂直的直线的方程;
(3)设过点
的直线交抛物线
于
、
两点,
,记
和
两点间的距离为
,求
关于
的表达式.
设锐角三角形 的内角
的内角 的对边分别为
的对边分别为 ,
, .
.
(1)求 的大小;
的大小;
(2)若 ,
, ,求
,求 .
.
已知△ABC的三个顶点 ,其外接圆为圆H.
,其外接圆为圆H.
(1)求圆H的方程;
(2)若直线l过点C,且被圆H截得的弦长为2,求直线l的方程;
(3)对于线段BH上的任意一点P,若在以C为圆心的圆上都存在不同的两点M、N,使得点M是线段PN的中点,求圆C的半径r的取值范围.
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
4 |
16 |
40 |
32 |
8 |
(1)在答题卡上作出这些数据的频率分布直方图;(用阴影涂黑) 
(2)估计这种产品质量指标值的平均数及中位数;
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的75%”的规定?
已知 的顶点
的顶点 ,
,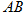 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为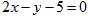 ,
,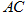 边上的高
边上的高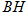 所在的直线方程为
所在的直线方程为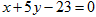 ,求:
,求:
(1)顶点 的坐标;
的坐标;
(2)直线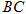 的方程.
的方程.
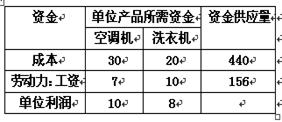
某卖场同时销售变频冷暖空调机和智能洗衣机,这两种产品的市场需求量大,有多少卖多少。今年元旦假期7天该卖场要根据实际情况确定产品的进货数量,以达到总利润最大。已知两种产品直接受资金和劳动力的限制。根据过去销售情况,得到两种产品的有关数据如下表:(表中单位:百元)
试问:怎样确定两种货物的进货量,才能使7天的总利润最大,最大利润是多少?