已知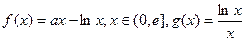 ,其中
,其中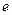 是自然常数,
是自然常数,
(Ⅰ)讨论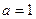 时,
时,  的单调性、极值;
的单调性、极值;
(Ⅱ)求证:在(Ⅰ)的条件下, ;
;
(Ⅲ)是否存在实数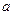 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出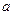 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知椭圆 的焦点分别为F1(
的焦点分别为F1( ,0)、F2(
,0)、F2( ,0),长轴长为6,设直线
,0),长轴长为6,设直线 交椭圆
交椭圆 于A、B两点.
于A、B两点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)求 的面积.
的面积.
f(x)=x3+ax2+bx+c在x=1与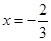 时,都取得极值.
时,都取得极值.
(1)求a,b的值;
(2)若 ,求f(x)的单调区间和极值.
,求f(x)的单调区间和极值.
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC 的中点.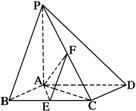
(Ⅰ)求证:AE⊥PD;
(Ⅱ)若直线PB与平面PAD所成角的正弦值为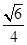 ,求二面角 E-AF-C的余弦值.
,求二面角 E-AF-C的余弦值.
正项数列{an}满足 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an.
(2)令bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=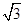 acosB.
acosB.
(1)求角B的大小;
(2)若a=2,△ABC的面积为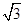 ,求b,c.
,求b,c.