(本小题满分12分)
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程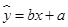 ;
;
(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量.(温馨提示:答题前请仔细阅读卷首所给出的计算公式)
已知数列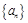 的首项
的首项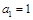 ,前n项之和
,前n项之和 满足关系式:
满足关系式: .
.
(1)求证:数列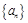 是等比数列;
是等比数列;
(2)设数列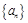 的公比为
的公比为 ,数列
,数列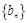 满足
满足 ,且
,且 .
.
(i)求数列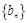 的通项
的通项 ;
;
(ii)设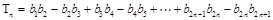 ,求
,求 .
.
咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
已知数列 中,
中, .
.
(1)设 ,求证:数列
,求证:数列 是常数列,并写出其通项公式;
是常数列,并写出其通项公式;
(2)设 ,求证:数列
,求证:数列 是等比数列,并写出其通项公式;
是等比数列,并写出其通项公式;
(3)求数列 的通项公式.
的通项公式.
函数 的图象如图所示.
的图象如图所示.
(1)求函数 的解析式;
的解析式;
(2)已知 ,求
,求 的值.
的值.