2011.年广州亚运会的一组志愿者全部通晓中文,并且每个志愿者还都通晓英语、日语和韩语中的一种(但无人通晓两种外语).已知从中任抽一人,其通晓中文和英语的概率为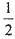 ,通晓中文和日语的概率为
,通晓中文和日语的概率为 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.
(I )求这组志愿者的人数;
(II)现从这组志愿者中选出通晓英语的志愿者1名,通晓韩语的志愿者1名,若甲通晓英语,乙通晓韩语,求甲和乙不全被选中的概率.
己知函数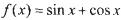 .
.
(I )若,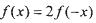 ,求
,求 的值;
的值;
(II)求函数 的最大值和单调递增区间.
的最大值和单调递增区间.
如图,椭圆的中心在坐标原点,长轴端点为A,B,右焦点为F,且 .
.
(I) 求椭圆的标准方程;
(II)过椭圆的右焦点F作直线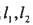 ,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且
,直线l1与椭圆分别交于点M,N,直线l2与椭圆分别交于点P,Q,且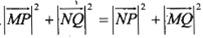 ,求四边形MPNQ的面积S的最小值.
,求四边形MPNQ的面积S的最小值.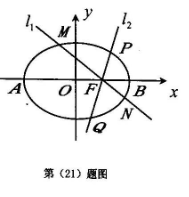
设M是由满足下列条件的函数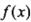 构成的集合:①方程,
构成的集合:①方程, 有实数根②函数
有实数根②函数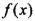 的导数
的导数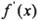 满足
满足 .
.
(I) 若函数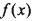 为集合M中的任意一个元素,证明:方程
为集合M中的任意一个元素,证明:方程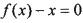 只有一个实数根;
只有一个实数根;
(II) 判断函数 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(III) 设函数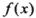 为集合M中的任意一个元素,对于定义域中任意
为集合M中的任意一个元素,对于定义域中任意 ,当
,当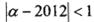 ,且
,且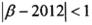 时,证明:
时,证明: .
.
如图,在多面体ABCDEFG中,四边形ABCD是边长为2的正方形,平面ABG、平面ADF、平面CDE都与平面ABCD垂直,且ΔABG, ΔADF,ΔCDE都是正三角形.
(I)求证:AC// EF;
(II) 求多面体ABCDEFG的体积.