有外形相同的球分装三个盒子,每盒10个,其中,第一个盒子中7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中则有红球8个,白球2个.试验按如下规则进行:先在第一个盒子中任取一球,若取得标有字母A的球,则在第二个盒子中任取一球;若第一次取得标有字母B的球,则在第三个盒子中任取一球.若第二次取出的是红球,则称试验成功.求试验成功的概率.
(本小题13分)曲线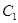 上任意一点M满足
上任意一点M满足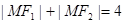 , 其中F
, 其中F (-
(-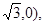 F
F (
(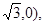 抛物线
抛物线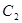 的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
的焦点是直线y=x-1与x轴的交点, 顶点为原点O.
(1)求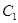 ,
,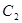 的标准方程;
的标准方程;
(2)请问是否存在直线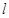 满足条件:①过
满足条件:①过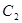 的焦点
的焦点 ;②与
;②与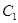 交于不同
交于不同
两点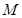 ,
, ,且满足
,且满足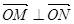 ?若存在,求出直线
?若存在,求出直线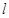 的方程;若不
的方程;若不
存在,说明理由.
(本小题12分)设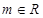 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
,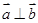 ,动点
,动点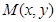 的轨迹为E.求轨迹E的方程,并说明该方程所表示曲线的形状.
的轨迹为E.求轨迹E的方程,并说明该方程所表示曲线的形状.
(本小题12分)已知p: ,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
,q:x2-2x+1-m2≤0(m>0),且┐p是┐q的必要而不充分条件,求实数m的取值范围.
(本小题12分)已知直线l与两坐标轴围成的三角形的面积为3, 且过定点A(-3,4). 求直线l的方程.
本小题12分)命题p: 函数y= 在(-1, +
在(-1, + )上单调递增, 命题
)上单调递增, 命题 函数y=lg[
函数y=lg[ ]的定义域为R
]的定义域为R
(1) 若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围;
的取值范围;
(2) 若“ 或
或 ”为真命题,“
”为真命题,“ 且
且 ”为假命题,求
”为假命题,求 的取值范围
的取值范围