(本小题满分12分)椭圆 的中心为坐标原点
的中心为坐标原点 ,焦点在
,焦点在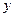 轴上,焦点到相应准线的距离以及离心率均为
轴上,焦点到相应准线的距离以及离心率均为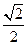 ,直线
,直线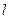 与
与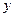 轴交于点
轴交于点 ,与椭圆
,与椭圆 交于相异两点
交于相异两点 、
、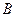 ,且
,且 .(1)求椭圆方程;(2)若
.(1)求椭圆方程;(2)若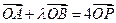 ,求
,求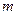 的取值范围.
的取值范围.
(本题12分).如图,四棱柱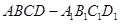 中,侧棱
中,侧棱 ⊥底面ABCD,AB//DC,AB⊥AD,AD=CD=1,
⊥底面ABCD,AB//DC,AB⊥AD,AD=CD=1, =AB=2,E为棱
=AB=2,E为棱 的中点.
的中点.
(Ⅰ)证明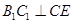
(Ⅱ)求二面角 的正弦值.
的正弦值.
(Ⅲ)设点M在线段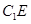 上,且直线AM与平面
上,且直线AM与平面 所成角的正弦值为
所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
(本题12分)如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=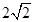 ,动点D在线段AB上.
,动点D在线段AB上.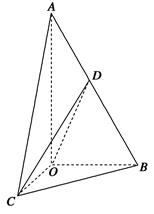
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
(本题12分)如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求四棱锥P—ABCD的表面积S.
(本题12分)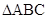 的内角
的内角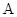 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,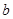 ,
,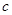 .向量
.向量 与
与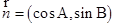 平行.
平行.
(Ⅰ)求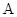 ;
;
(Ⅱ)若 ,
, ,求
,求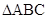 的面积.
的面积.
(本题10分)已知不等式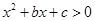 的解集为
的解集为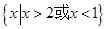 .
.
(1)求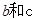 的值;
的值;
(2)求不等式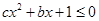 的解集
的解集