已知向量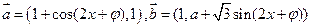 (
( 为常数且
为常数且 ),函数
),函数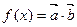 在
在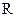 上的最大值为
上的最大值为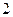 .
.
(1)求实数 的值;
的值;
(2)把函数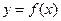 的图象向右平移
的图象向右平移 个单位,可得函数
个单位,可得函数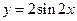 的图象,求函数
的图象,求函数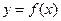 的解析式及其单调增区间.
的解析式及其单调增区间.
【2015高考山东,理19】若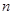 是一个三位正整数,且
是一个三位正整数,且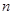 的个位数字大于十位数字,十位数字大于百位数字,则称
的个位数字大于十位数字,十位数字大于百位数字,则称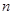 为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得
为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得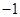 分;若能被10整除,得1分.
分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的“三位递增数” ;
(Ⅱ)若甲参加活动,求甲得分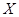 的分布列和数学期望
的分布列和数学期望 .
.
【2015高考福建,理16】某银行规定,一张银行卡若在一天内出现3次密码尝试错误,该银行卡将被锁定,小王到银行取钱时,发现自己忘记了银行卡的密码,但是可以确定该银行卡的正确密码是他常用的6个密码之一,小王决定从中不重复地随机选择1个进行尝试.若密码正确,则结束尝试;否则继续尝试,直至该银行卡被锁定.
(Ⅰ)求当天小王的该银行卡被锁定的概率;
(Ⅱ)设当天小王用该银行卡尝试密码次数为X,求X的分布列和数学期望.
【2015高考新课标2,理18】
某公司为了解用户对其产品的满意度,从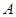 ,
,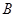 两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);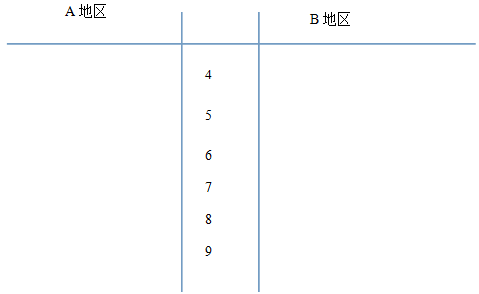
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
| 满意度评分 |
低于70分 |
70分到89分 |
不低于90分 |
| 满意度等级 |
不满意 |
满意 |
非常满意 |
记时间C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
【2015高考上海,理22】已知数列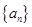 与
与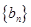 满足
满足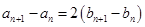 ,
,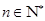 .
.
(1)若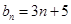 ,且
,且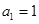 ,求数列
,求数列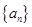 的通项公式;
的通项公式;
(2)设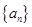 的第
的第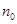 项是最大项,即
项是最大项,即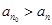 (
(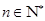 ),求证:数列
),求证:数列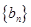 的第
的第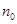 项是最大项;
项是最大项;
(3)设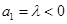 ,
,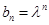 (
(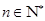 ),求
),求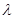 的取值范围,使得
的取值范围,使得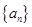 有最大值
有最大值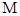 与最小值
与最小值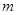 ,且
,且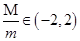 .
.
【2015高考广东,理21】数列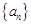 满足
满足 ,
,
(1)求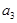 的值;
的值;
(2)求数列 前
前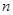 项和
项和 ;
;
(3)令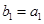 ,
,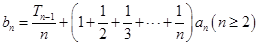 ,证明:数列
,证明:数列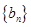 的前
的前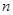 项和
项和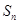 满足
满足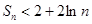 .
.