已知i,m、n是正整数,且1<i≤m<n.
(1)证明: niA <miA
<miA

(2)证明: (1+m)n>(1+n)m
椭圆
的离心率
.
(1)求椭圆
的方程;
(2)如图,
是椭圆
的顶点,
是椭圆
上除顶点外的任意一点,直线
交
轴于点
,直线
交
于点
.设
的斜率为
,
的斜率为
.证明:
为定值.
如图,直四棱柱 中, , , , , , 为 上一点, ,

(1)证明:
平面
;
(2)求点
到平面
的距离。
小波以游戏方式决定是去打球、唱歌还是去下棋。游戏规则为:以
为起点,再从
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
,若
就去打球,若
就去唱歌,若
就去下棋。
(1)写出数量积
的所有可能值;
(2)分别求小波去下棋的概率和不去唱歌的概率。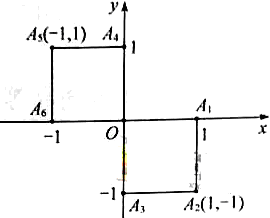
在 中,角 的对边分别是 ,已知 .
(1)求证: 成等差数列;
(2)若
,求
的值.
正项数列 .