如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程. 
已知曲线C上的动点P(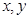 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
(1)求曲线C的方程。
(2)过点M(1,2)的直线 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。
已知下列三个方程: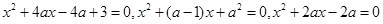 至少有一个方程有实数根.求实数
至少有一个方程有实数根.求实数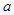 的取值范围.
的取值范围.
设命题p:实数x满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
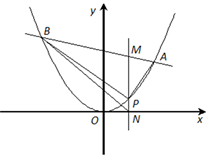
如图已知抛物线 :
: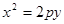 过点
过点 ,直线
,直线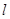 交
交 于
于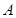 ,
,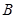 两点,过点
两点,过点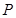 且平行于
且平行于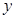 轴的直线分别与直线
轴的直线分别与直线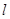 和
和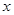 轴相交于点
轴相交于点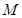 ,
, .
.
(1)求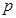 的值;
的值;
(2)是否存在定点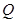 ,当直线
,当直线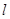 过点
过点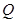 时,△
时,△ 与△
与△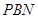 的面积相等?若存在,求出点
的面积相等?若存在,求出点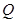 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知中心在坐标原点,焦点在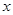 轴上的椭圆过点
轴上的椭圆过点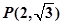 ,且它的离心率
,且它的离心率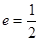 .
.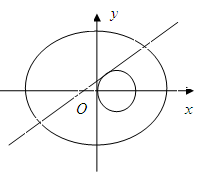
(1)求椭圆的标准方程;
(2)与圆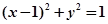 相切的直线
相切的直线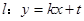 交椭圆于
交椭圆于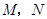 两点,若椭圆上一点
两点,若椭圆上一点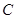 满足
满足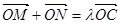 ,求实数
,求实数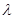 的取值范围.
的取值范围.