已知斜三棱柱ABC—A1B1C1中,A1C1=B1C1=2,D、D1分别是AB、A1B1的中点,平面A1ABB1⊥平面A1B1C1,异面直线AB1和C1B互相垂直.
(1)求证: AB1⊥C1D1;
(2)求证: AB1⊥面A1CD;
(3)若AB1=3,求直线AC与平面A1CD所成的角. 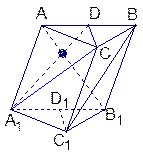
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为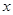 元,
元,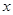 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润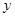 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格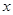 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每纪念章销售价格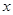 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润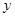 (元)最大,并求出最大值.
(元)最大,并求出最大值.
已知集合 与
与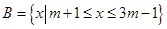 分别是函数
分别是函数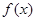 的定义域与值域.
的定义域与值域.
(1)求集合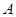 ;
;
(2)当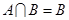 时,求实数
时,求实数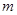 的取值范围.
的取值范围.
(1)计算: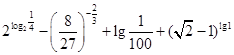
(2)已知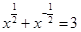 ,求
,求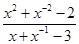 的值.
的值.
矩形 的中心在坐标原点,边
的中心在坐标原点,边 与
与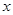 轴平行,
轴平行,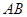 =8,
=8, =6.
=6.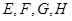 分别是矩形四条边的中点,
分别是矩形四条边的中点,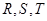 是线段
是线段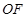 的四等分点,
的四等分点,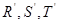 是线段
是线段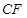 的四等分点.设直线
的四等分点.设直线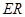 与
与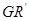 ,
,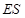 与
与 ,
, 与
与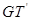 的交点依次为
的交点依次为 .
.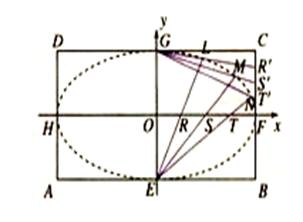
(1)求以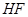 为长轴,以
为长轴,以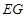 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段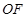 的
的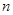 (
(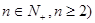 等分点从左向右依次为
等分点从左向右依次为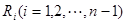 ,线段
,线段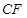 的
的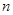 等分点从上向下依次为
等分点从上向下依次为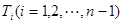 ,那么直线
,那么直线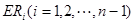 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
某种汽车的购车费用是10万元,每年使用的保险费、养路费、汽油费约为 万元,年维修费用第一年是
万元,年维修费用第一年是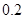 万元,第二年是
万元,第二年是 万元,第三年是
万元,第三年是 万元,…,以后逐年递增
万元,…,以后逐年递增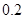 万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用
万元汽车的购车费用、每年使用的保险费、养路费、汽油费、维修费用的和平均摊到每一年的费用叫做年平均费用.设这种汽车使用 年的维修费用的和为
年的维修费用的和为 ,年平均费用为
,年平均费用为 .
.
(1)求出函数 ,
, 的解析式;
的解析式;
(2)这种汽车使用多少年时,它的年平均费用最小?最小值是多少?