设集合A={x|4x–2x+2+a=0,x∈R}.
(1)若A中仅有一个元素,求实数a的取值集合B;
(2)若对于任意a∈B,不等式x2–6x<a(x–2)恒成立,求x的取值范围.
数列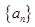 中,已知
中,已知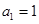 ,
, 时,
时, .数列
.数列 满足:
满足: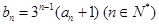 .
.
(1)证明: 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(2)记数列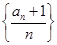 的前
的前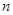 项和为
项和为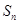 ,若不等式
,若不等式 成立(
成立( 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对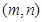 .
.
设椭圆 :
:  的离心率为
的离心率为 ,点
,点 (
( ,0),
,0), (0,
(0, )原点
)原点 到直线
到直线 的距离为
的距离为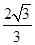 。
。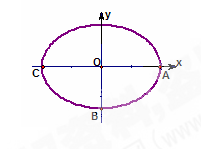
(1) 求椭圆 的方程;
的方程;
(2) 设点 为(
为( ,0),点
,0),点 在椭圆
在椭圆 上(与
上(与 、
、 均不重合),点
均不重合),点 在直线
在直线 上,若直线
上,若直线 的方程为
的方程为 ,且
,且 ,试求直线
,试求直线 的方程.
的方程.
设函数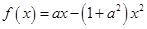 (
(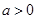 ).区间
).区间 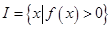 ,定义区间
,定义区间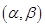 的长度为 b-a .
的长度为 b-a .
(1)求区间I的长度 (用 a 表示);
(用 a 表示);
(2)若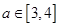 ,求
,求 的最大值.
的最大值.
设 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 的前
的前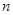 项和.已知
项和.已知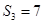 ,且
,且 构成等差数列.
构成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列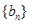 的前n项和
的前n项和 .
.
已知函数f(x)=ax2+bx+1(a,b为实数),x∈R,F(x)=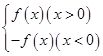
(1)若f(-1)=0,且函数f(x) ≥0的对任意x属于一切实数成立,求F(x)的表达式;
(2)在 (1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;