已知抛物线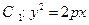 的准线方程为
的准线方程为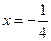 ,与直线
,与直线
在第一象限相交于点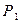 ,过
,过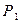 作
作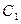 的切线
的切线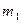 ,过
,过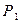 作
作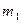 的垂线
的垂线 交x轴正
交x轴正
半轴于点 ,过
,过 作
作 的平行线
的平行线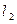 交抛物线于第一象限内的点
交抛物线于第一象限内的点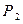 ,过
,过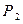 作
作
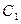 的切线
的切线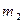 ,过
,过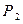 作
作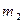 的垂线
的垂线 交x轴正半轴于点
交x轴正半轴于点 ,依此类推,在x
,依此类推,在x
轴上形成一点列 ,
, ,
,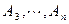 (
( )设
)设 的坐标为(
的坐标为( )
)
(Ⅰ)求抛物线的方程;(Ⅱ)试探求 关于
关于 的递推关系;
的递推关系;
(本小题满分12分)已知椭圆 的离心率为
的离心率为 ,直线
,直线 过点
过点 ,
, ,且与椭圆
,且与椭圆 相切于点
相切于点 .
.
(1)求椭圆 的方程;
的方程;
(2)是否存在过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 、
、 ,使得
,使得 ?若存在,试求出直线
?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
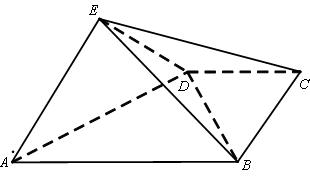
(本小题满分12分)(理科做)如图,四棱锥 中,平面
中,平面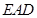
 平面
平面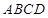 ,
,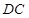 //
//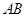 ,
, ,
, ,且
,且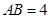 ,
,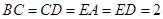 .
.
(1)求证: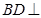 平面
平面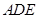 ;
;
(2)求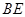 和平面
和平面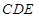 所成角的正弦值;
所成角的正弦值;
(3)在线段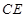 上是否存在一点
上是否存在一点 使得平面
使得平面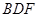
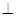 平面
平面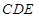 ,请说明理由.
,请说明理由.
(文科做)已知函数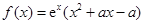 ,其中
,其中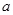 是常数.
是常数.
(1)当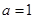 时,求曲线
时,求曲线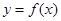 在点
在点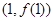 处的切线方程;
处的切线方程;
(2)若存在实数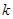 ,使得关于
,使得关于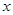 的方程
的方程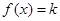 在
在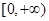 上有两个不相等的实数根,求
上有两个不相等的实数根,求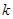 的取值范围.
的取值范围.
(本小题12分)在平面直角坐标系中,已知一个椭圆的中心在原点,左焦点为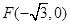 ,且过
,且过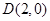 .
.
(1)求该椭圆的标准方程;
(2)若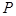 是椭圆上的动点,点
是椭圆上的动点,点 ,求线段
,求线段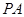 中点
中点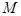 的轨迹方程.
的轨迹方程.
(本小题12分)为了了解某校高一学生体能情况,抽取200位同学进行1分钟跳绳次数测试,将所得数据整理后画出频率分布直方图(如图所示),请回答下列问题: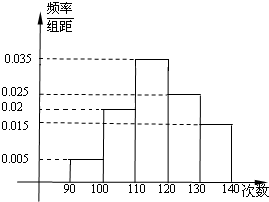
(1)次数在100~110之间的频率是多少?
(2)若次数在110以上为达标,试估计该校全体高一学生的达标率是多少?
(3)根据频率分布直方图估计,学生跳绳次数的平均数是多少?
(本小题12分)已知 ,
, ,点
,点 的坐标为
的坐标为 .
.
(1)求当 时,点
时,点 满足
满足 的概率;
的概率;
(2)求当 时,点
时,点 满足
满足 的概率.
的概率.