对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数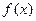 称为
称为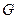 函数。
函数。
① 对任意的 ,总有
,总有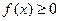 ;
;
② 当 时,总有
时,总有 成立。
成立。
已知函数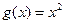 与
与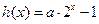 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数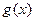 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数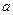 组成的集合;
组成的集合;
(3)在(2)的条件下,讨论方程
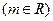 解的个数情况。
解的个数情况。
在长方体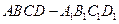 中,
中, 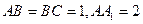 ,
,
点 是
是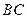 的中点,点
的中点,点 是
是 的中点.
的中点.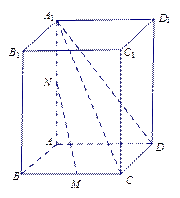
(Ⅰ)求证: 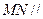 平面
平面 ;
;
(Ⅱ)求异面直线 和
和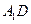 所成的角余弦值;
所成的角余弦值;
(Ⅲ)过 三点的平面把长方体
三点的平面把长方体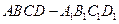 截成
截成
两部分几何体, 求所截成的两部分几何体的体积的比值.
设函数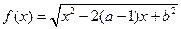 的定义域为
的定义域为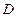 .
.
(I)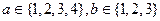 ,求使
,求使 的概率;
的概率;
(II) ,求使
,求使 的概率.
的概率.
已知△ 的周长为
的周长为 ,且
,且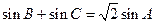 .
.
(1)求边长 的值;
的值;
(2)若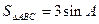 ,求
,求 的正切值.
的正切值.
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和
和 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数 的分布列与期望.
的分布列与期望.
已知向量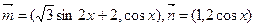 ,设函数
,设函数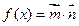 。
。
(1)求 的最小正周期与单调递减区间
的最小正周期与单调递减区间
(2)在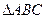 中,
中, 、
、 、
、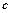 分别是角
分别是角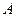 、
、 、
、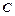 的对边,若
的对边,若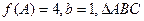 的面积为
的面积为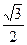 ,求
,求 的值。
的值。