(本小题满分12分)
某游乐园为迎接建国60周年,特在今年年初用98万元购进一批新的游乐器材供游客游玩。预计第一年包括维修费在内需各种费用12万元,从第二年开始每年所需费用均比前一年增加4万元,这些玩具每年总收入预计为50万元,若干年后,若有两种处理方案:①当盈利总额达到最大时,以8万元的价格全部卖出;②当年平均盈利达到最大值时,以26万元的价格全部卖出.
(Ⅰ)分别写出经过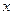 年后方案①中盈利总额
年后方案①中盈利总额 和方案②中年平均盈利y2关于x的函数关系式
和方案②中年平均盈利y2关于x的函数关系式
(Ⅱ)问哪一种方案较为划算?请说明理由 ?
设椭圆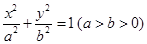 的左、右顶点分别为
的左、右顶点分别为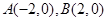 ,离心率
,离心率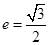 .过该椭圆上任一点
.过该椭圆上任一点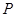 作
作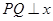 轴,垂足为
轴,垂足为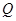 ,点
,点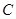 在
在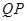 的延长线上,且
的延长线上,且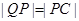 .
.
(1)求椭圆的方程;
(2)求动点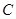 的轨迹
的轨迹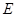 的方程;
的方程;
(3)设直线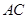 (
(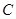 点不同于
点不同于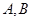 )与直线
)与直线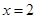 交于点
交于点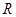 ,
,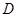 为线段
为线段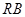 的中点,试判断直线
的中点,试判断直线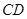 与曲线
与曲线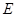 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
如下图,互相垂直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个更
,现欲将其扩建成一个更
大的三角形花园 ,要求点
,要求点 在射线
在射线 上,点
上,点 在射线
在射线 上,且直线
上,且直线 过点
过点 ,其中
,其中 米,
米, 米.记三角形花园
米.记三角形花园 的面积为
的面积为 .
.
(1)问: 取何值时,
取何值时, 取得最小值,并求出最小值;
取得最小值,并求出最小值;
(2)若 不超过1764平方米,求
不超过1764平方米,求 长的取值范围.
长的取值范围.
在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1)证明: ;
;
(2)证明: 平面
平面 ;
;
(3)(限理科生做,文科生不做)求二面角 的余弦值.
的余弦值.
已知命题 ,命题
,命题
 ,若
,若 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知函数 ,
, .
.
(1)求 的值;
的值;
(2)设
 求
求 的值.
的值.