跳台滑雪起源于娜威.1860年娜威德拉门地区的两位农民在奥斯陆举行的首届全国滑雪比赛上表演了跳台飞跃动作,后逐渐成为一个独立的项目并得到推广.图为一跳台的示意图,运动员从雪道的最高点A由静止开始滑下,不借助其他器械,沿雪道滑到跳台B点后,沿与水平方向成300角斜向左上方飞出,最后落在斜坡上C点.已知A、B两点间高度差为4 m,B、C点两间高度差为13 m,运动员从B点飞出时速度为8 m/s,运动员连同滑雪装备总质量为60 kg.不计空气阻力,g="10" m/s2.求:
(1)运动员从B点飞出时的动能;
(2)从最高点A滑到B点的过程中,运动员克服摩擦阻力做的功;
(3)运动员落到C点时的速度;
(4)离开B点后,在距C点多高时,运动员的重力势能等于动能.(以C点为零势能参考面)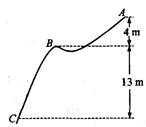
如图所示,长5m的水平传送带以2m/s的速度匀速运动,物体与传送带间的动摩擦因数为μ=0.1。现将物体轻轻地放到传送带的A端,那么,物体从A端到B端的过程中,摩擦力存在的时间有多长?方向如何?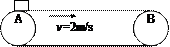
一根大弹簧内套一根小弹簧,大弹簧比小弹簧长0.2m,它们的下端平齐并固定,另一端自由,如图所示.当压缩此组合弹簧时,测得弹力与弹簧压缩量的关系如图所示.试求这两根弹簧的劲度系数k1和k2

如图所示,矩形均匀薄板长AC = 60cm,宽CD = 10cm.在B点以细线悬挂,板处于平衡,AB = 35cm,则悬线和板边缘CA的夹角α等于多少?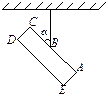
如图所示,有一等边三角形ABC,在B、C两点各放一个质量为m的小球,在A处放一个质量为2m的小球,求这三个球所组成的系统的重心在何处.
某种汽车的制造标准是车身在横向倾斜300角时不翻倒,如图所示。若车轮间距离为2m,那么车身重心G离斜面的高度应不超过多少米?