已知数列 的通项公式为
的通项公式为 .
.
(1)试问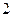 是否是数列
是否是数列 中的项?
中的项?
(2)若 ,求
,求 .
.
安徽理)(如图,圆锥顶点为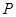 。底面圆心为
。底面圆心为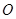 ,其母线与底面所成的角为
,其母线与底面所成的角为 。
。 和
和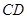 是底面圆
是底面圆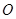 上的两条平行的弦,轴
上的两条平行的弦,轴 与平面
与平面 所成的角为
所成的角为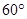 ,
, 
(1)证明:平面 与平面
与平面 的交线平行于底面;
的交线平行于底面;
(2)求 。
。
安徽理)(设椭圆 的焦点在
的焦点在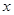 轴上
轴上
(1)若椭圆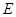 的焦距为1,求椭圆
的焦距为1,求椭圆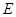 的方程;
的方程;
(2)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,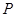 为椭圆
为椭圆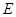 上第一象限内的点,直线
上第一象限内的点,直线 交
交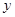 轴与点
轴与点 ,并且
,并且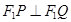 ,证明:当
,证明:当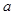 变化时,点
变化时,点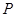 在某定直线上。
在某定直线上。
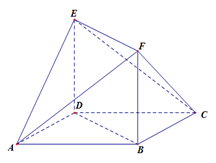
如图所示的多面体中,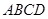 是菱形,
是菱形,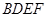 是矩形,
是矩形,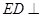 面
面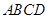 ,
,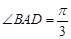 .
.
(1)求证:平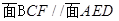 ;
;
(2)若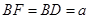 ,求四棱锥
,求四棱锥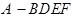 的体积.
的体积.
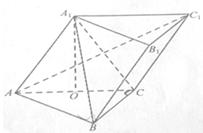
如图,在斜三棱柱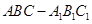 中,O是AC的中点,
中,O是AC的中点,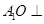 平面
平面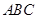 ,
,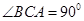 ,
,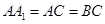 .
.
(1)求证: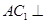 平面
平面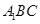 ;
;
(2)求二面角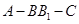 的余弦值.
的余弦值.
如图,三棱锥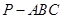 中,
中,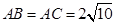 ,
,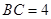 ,
,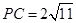 ,点
,点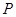 在平面
在平面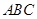 内的射影恰为
内的射影恰为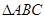 的重心
的重心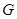 ,M为侧棱
,M为侧棱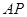 上一动点.
上一动点.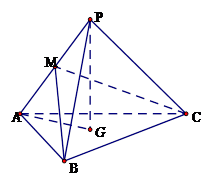
(1)求证:平面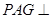 平面
平面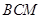 ;
;
(2)当M为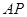 的中点时,求直线
的中点时,求直线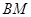 与平面
与平面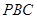 所成角的正弦值.
所成角的正弦值.