已知点 到两个定点
到两个定点 距离的比为
距离的比为 ,点
,点 到直线
到直线 的距离为1.求直线
的距离为1.求直线 的方程.
的方程.
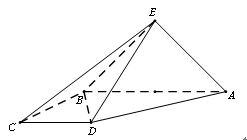
(本小题满分12分)如图,直角梯形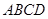 与等腰直角三角形
与等腰直角三角形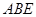 所在的平面互相垂直.
所在的平面互相垂直.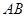 ∥
∥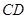 ,
,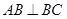 ,
,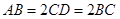 ,
,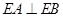 .
.
(1)求直线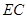 与平面
与平面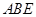 所成角的正弦值;
所成角的正弦值;
(2)线段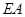 上是否存在点
上是否存在点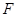 ,使
,使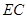 // 平面
// 平面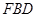 ?若存在,求出
?若存在,求出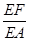 ;若不存在,说明理由.1
;若不存在,说明理由.1
某商场共五层,从五层下到四层有3个出口,从三层下到二层有4个出口,从二层下到一层有4个出口,从一层走出商场有6个出口。安全部门在每层安排了一名警员值班,负责该层的安保工作。假设每名警员到该层各出口处的时间相等,某罪犯在五楼犯案后,欲逃出商场,各警员同时接到指令,选择一个出口进行围堵。逃犯在每层选择出口是等可能的。已知他被三楼警员抓获的概率为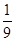 。
。
(Ⅰ)问四层下到三层有几个出口?
(Ⅱ)天网恢恢,疏而不漏,犯罪嫌疑人最终落入法网。设抓到逃犯时,他已下了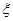 层楼,写出
层楼,写出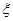 的分布列,并求
的分布列,并求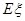 。
。
已知函数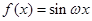
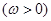 在区间
在区间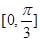 上单调递增,在区间
上单调递增,在区间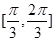 上单调递减;如图,四边形
上单调递减;如图,四边形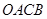 中,
中,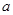 ,
,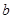 ,
,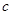 为
为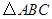 的内角
的内角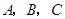 的对边,
的对边,
且满足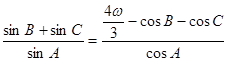 .
.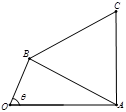
(Ⅰ)证明: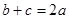 ;
;
(Ⅱ)若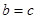 ,设
,设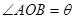 ,
,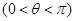 ,
,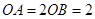 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
已知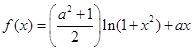
 .
.
(1)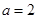 时,求
时,求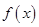 的极值;
的极值;
(2)当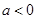 时,讨论
时,讨论 的单调性;
的单调性;
(3)证明: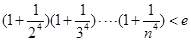 (
(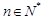 ,
,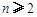 ,其中无理数
,其中无理数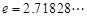 )
)
已知点是F抛物线 与椭圆
与椭圆 的公共焦点,且椭圆的离心率为
的公共焦点,且椭圆的离心率为

(1)求椭圆的方程;
(2)过抛物线上一点P,作抛物线的切线 ,切点P在第一象限,如图,设切线
,切点P在第一象限,如图,设切线 与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为
与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为 (其中
(其中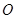 为坐标原点),若
为坐标原点),若 ,求点P的坐标.
,求点P的坐标.