求以相交两圆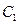 :
: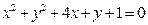 及
及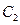 :
: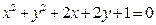 的公共弦为直径的圆的方程.
的公共弦为直径的圆的方程.
某厂生产的圆柱形零件的外直径ξ服从正态分布N(4,0.25),质检人员从该厂生产的1000件零件中随机抽查一件,测得它的外直径为5.7cm,试问该厂生产的这批零件是否合格?
已知正态总体N(1,4),.求F(3)。
某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?
若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高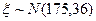 (单位:㎝),则该地公共汽车门的高度应设计为多高?
(单位:㎝),则该地公共汽车门的高度应设计为多高?
已知:从某批材料中任取一件时,取得的这件材料强度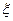 服从
服从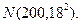
(1)计算取得的这件材料的强度不低于180的概率.
(2)如果所用的材料要求以99%的概率保证强度不低于150,问这批材料是否符合这个要求.