已知点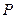 在椭圆
在椭圆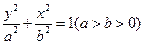 上,
上,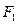 ,
,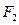 为椭圆的两个焦点,求
为椭圆的两个焦点,求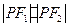 的取值范围.
的取值范围.
已知数列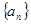 是公差为1的等差数列,
是公差为1的等差数列,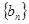 是公比为2的等比数列,
是公比为2的等比数列,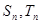 分别是数列
分别是数列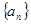 和
和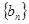 前n项和,且
前n项和,且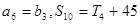
①分别求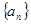 ,
,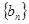 的通项公式。
的通项公式。
②若 ,求n的范围
,求n的范围
③令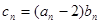 ,求数列
,求数列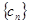 的前n项和
的前n项和 。
。
六名学生需依次进行身体体能和外语两个项目的训练及考核。每个项目只有一次补考机会,补考不合格者不能进入下一个项目的训练(即淘汰),若每个学生身体体能考核合格的概率是 ,外语考核合格的概率是
,外语考核合格的概率是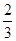 ,假设每一次考试是否合格互不影响。
,假设每一次考试是否合格互不影响。
①求某个学生不被淘汰的概率。
②求6名学生至多有两名被淘汰的概率
③假设某学生不放弃每一次考核的机会,用 表示其参加补考的次数,求随机变量
表示其参加补考的次数,求随机变量 的分布列和数学期望。
的分布列和数学期望。
在正三棱柱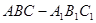 中,底面三角形ABC的边长为
中,底面三角形ABC的边长为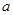 ,侧棱的长为
,侧棱的长为 ,D为棱
,D为棱 的中点。
的中点。
①求证: ∥平面
∥平面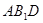
②求二面角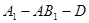 的大小
的大小
③求点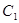 到平面
到平面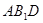 的距离。
的距离。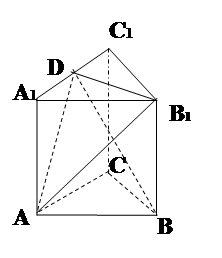
在锐角△ABC中,角A,B,C的对边分别为a,b,c,已知 ,
, 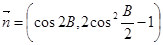 ,且
,且 ∥
∥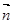
①求角B的大小②若b=1,求△ABC面积的最大值。
已知函数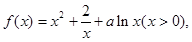
(Ⅰ)若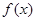 在
在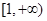 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)若定义在区间D上的函数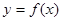 对于区间D上的任意两个值
对于区间D上的任意两个值 总有以下不等式
总有以下不等式 成立,则称函数
成立,则称函数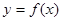 为区间D上的“下凸函数”.
为区间D上的“下凸函数”.
试证当 时,
时,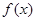 为“下凸函数”.
为“下凸函数”.