在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率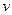 (单位:cm
(单位:cm /s)与管道半径
/s)与管道半径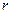 (单位:cm)的四次方成正比.
(单位:cm)的四次方成正比.
(1) 写出气流速度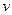 关于管道半径
关于管道半径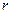 的函数解析式;
的函数解析式;
(2) 若气体在半径为3cm的管道中,流量速率为400cm /s,求该气体通过半
/s,求该气体通过半
径为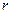 的管道时,其流量速率
的管道时,其流量速率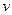 的表达式;
的表达式;
(3) 已知(2)中的气体通过的管道半径为5cm,计算该气体的流量速率.
一批食品,每袋的标准重量是50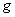 ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:
,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位: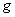 ),并得到其茎叶图(如图).
),并得到其茎叶图(如图).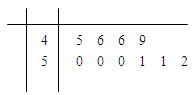
(1)求这10袋食品重量的众数,并估计这批食品实际重量的平均数;
(2)若某袋食品的实际重量小于或等于47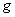 ,则视为不合格产品,试估计这批食品重量的合格率.
,则视为不合格产品,试估计这批食品重量的合格率.
已知函数 (
(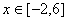 )的图象如图.根据图象写出:
)的图象如图.根据图象写出: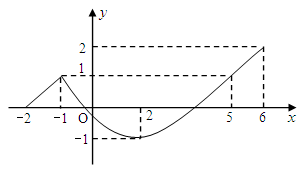
(1)函数 的最大值;
的最大值;
(2)使 的
的 值.
值.
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数 的分布列及数学期望
的分布列及数学期望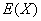
二项式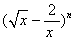 的展开式中:
的展开式中:
(1)若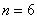 ,求倒数第二项
,求倒数第二项
(2)若第5项与第3项的系数比为 ,求各项的二项式系数和。
,求各项的二项式系数和。
为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| 男 |
女 |
|
| 爱好 |
40 |
30 |
| 不爱好 |
160 |
270 |
(1)估计该地区大学生中,爱好该项运动的大学生的比例;
(2)能否有99%的把握认为该地区的大学生是否爱好该项体育运动与性别有关?
附: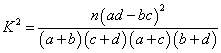
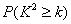 |
0.050 |
0.010 |
0.001 |
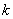 |
3.841 |
6.635 |
10.828 |