 位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道
位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道 题中任选一题作答,选甲题答对得
题中任选一题作答,选甲题答对得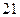 分,答错得
分,答错得 分;选乙题答对得
分;选乙题答对得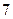 分,答错得
分,答错得 分.若
分.若 位同学的总分为
位同学的总分为 ,求这
,求这 位同学不
位同学不 同得分情况的种数。
同得分情况的种数。
设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+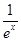 ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
已知椭圆C: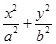 =1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
=1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
(1)求椭圆C的方程;
(2)过右焦点F2的斜率为k(k≠0)的直线l与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′,求证: k·k′为定值.
设数列{an}的各项都是正数,且对任意n∈N*,都有 +…+
+…+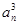 =
= ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.
(1)求数列{an}的通项公式;
(2)若bn=3n+(-1)n-1λ·2an(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有bn+1>bn.
如图,已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=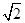 .
.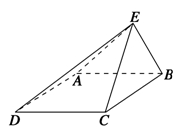
(1)求证:平面EAB⊥平面ABCD;
(2)求直线AE与平面CDE所成角的正弦值.
市民李先生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立.假设李先生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路A,B,D上下班时间往返出现拥堵的概率都是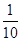 ,道路C,E上下班时间往返出现拥堵的概率都是
,道路C,E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.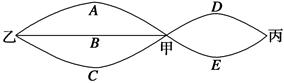
(1)求李先生的小孩按时到校的概率;
(2)李先生是否有七成把握能够按时上班?
(3)设X表示李先生下班时从单位乙到达小学丙遇到拥堵的次数,求X的均值.