(本小题满分12分)某食品企业一个月内被消费者投诉的次数用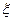 表示,
表示,
椐统计,随机变量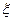 的概率分布如下:
的概率分布如下:
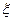 |
0 |
1 |
2 |
3 |
| p |
0.1 |
0.3 |
2a |
a |
(Ⅰ)求a的值和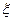 的数学期望;
的数学期望;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到 列联表如下:
列联表如下:
| 室外工作 |
室内工作 |
合计 |
|
| 有呼吸系统疾病 |
150 |
||
| 无呼吸系统疾病 |
100 |
||
| 合计 |
200 |
(1)补全 列联表;
列联表;
(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
已知函数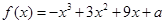 ,
,
(1)求 的单调递减区间;
的单调递减区间;
(2)若 在区间
在区间 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值.
已知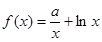 ,
,  ,
,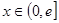 ,其中e是无理数且e="2.71828" ,
,其中e是无理数且e="2.71828" ,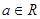 .
.
(1)若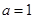 ,求
,求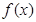 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下, ;
;
(3)是否存在实数a,使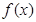 的最小值是
的最小值是 ?若存在,求出a的值;若不存在,说明理由.
?若存在,求出a的值;若不存在,说明理由.
设数列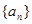 的前n项和为
的前n项和为 ,且
,且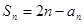 (
( ).
).
(1)求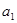 ,
,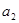 ,
, ,
,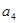 的值;
的值;
(2)猜想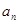 的表达式,并加以证明。
的表达式,并加以证明。
某学校高一年级组建了A、B、C、D四个不同的“研究性学习”小组,要求高一年级学生必须参加,
且只能参加一个小组的活动.假定某班的甲、乙、丙三名同学对这四个小组的选择是等可能的.
(1)求甲、乙、丙三名同学选择四个小组的所有选法种数;
(2)求甲、乙、丙三名同学中至少有二人参加同一组活动的概率;
(3)设随机变量X为甲、乙、丙三名同学参加A小组活动的人数,求X的分布列与数学期望EX.