(2009陕西卷文)(本小题满分12分)
椐统计,某食品企业一个月内被消费者投诉的次数为0,1,2的概率分别为0.4,0.5,0.1
(Ⅰ) 求该企业在一个月内共被消费者投诉不超过1次的概率;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
如右放置在水平面上的组合体由直三棱柱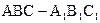 与正三棱锥
与正三棱锥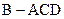 组成,其中,
组成,其中,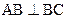 .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为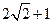 ,
,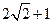 ,
,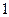 .
.
(Ⅰ)求直线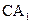 与平面
与平面 所成角的正弦;
所成角的正弦;
(Ⅱ)在线段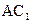 上是否存在点
上是否存在点 ,使
,使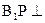 平面
平面 .若存在,确定点
.若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
图①是一个正方体的表面展开图,MN和PQ是两条面对角线,请在图(2)的正方体中将MN,PQ画出来,并就这个正方体解答下列各题:
(1)求MN和PQ所成角的大小;
(2)求四面体M—NPQ的体积与正方体的体积之比;
(3)求二面角M—NQ—P的大小。
已知长方体ABCD—A1B1C1D1中,AB=BC=4,AA1=8,E、F分别为AD和CC1的中点,O1为下底面正方形的中心。
(Ⅰ)证明:AF⊥平面FD1B1;
(Ⅱ)求异面直线EB与O1F所成角的余弦值;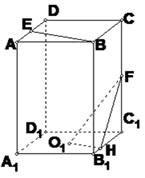
如图,直四棱柱ABCD-A1B1C1D1的底面是
梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别是CC1、C1D1的中点。点P到直线
AD1的距离为
⑴求证:AC∥平面BPQ
⑵求二面角B-PQ-D的大小
在直三棱柱ABC—A1B1C1中,CA=CB=CC1=2,∠ACB=90°,E、F分别是BA、BC的中点,G是AA1上一点,且AC1⊥EG.
(Ⅰ)确定点G的位置;
(Ⅱ)求直线AC1与平面EFG所成角θ的大小. 