(2009福建卷文)(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果; 

(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若 ,
, 是椭圆
是椭圆 上关
上关 轴对称的任意两点,设点
轴对称的任意两点,设点 ,连接
,连接 交椭圆
交椭圆 于另一点
于另一点 ,求证:直线
,求证:直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)设 为坐标原点,在(Ⅱ)的条件下,过点
为坐标原点,在(Ⅱ)的条件下,过点 的直线交椭圆
的直线交椭圆 于
于 ,
, 两点,求
两点,求 的取值范围.
的取值范围.
已知数列 的前n项和
的前n项和 (
( ),数列
),数列
 .
.
(Ⅰ)求证:数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前n项和为
的前n项和为 ,证明:
,证明: 且
且 时,
时,

 ;
;
(Ⅲ)设数列 满足
满足 ,(
,( 为非零常数,
为非零常数, ),问是否存在整数
),问是否存在整数 ,使得对任意
,使得对任意  ,都有
,都有 ?
?
已知函数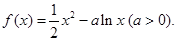
(Ⅰ)若 求
求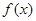 在
在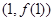 处的切线方程;
处的切线方程;
(Ⅱ)求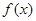 在区间
在区间 上的最小值;
上的最小值;
(Ⅲ)若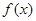 在区间
在区间 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围.
如图,在四棱锥 中,底面
中,底面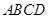 是边长为
是边长为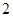 的正方形,侧面
的正方形,侧面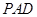
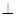 底面
底面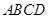 ,且
,且 ,
,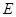 、
、 分别为
分别为 、
、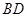 的中点.
的中点.
(Ⅰ)求证: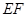 //平面
//平面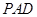 ;
;
(Ⅱ)求证:平面
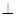 平面
平面 ;
;
(Ⅲ)在线段 上是否存在点
上是否存在点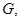 使得二面角
使得二面角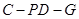 的余弦值为
的余弦值为 ?若存在,求
?若存在,求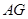 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
在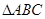 中,
中,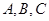 的对边分别为
的对边分别为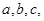 且
且 成等差数列.
成等差数列.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的范围.
的范围.