2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》.某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网.据测算,2001年该市用于“校校通”工程的经费为500万元.为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元.那么从2001年起的未来10 年内,该市在“校校通”工程中的总投入是多少?
(本小题满分12分)已知椭圆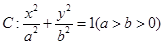 的左右焦点分别是
的左右焦点分别是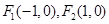 ,直线
,直线 的方程是
的方程是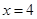 ,点
,点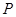 是椭圆
是椭圆 上动点(不在
上动点(不在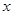 轴上),过点
轴上),过点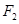 作直线
作直线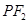 的垂线交直线
的垂线交直线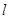 于点
于点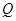 ,当
,当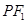 垂直
垂直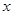 轴时,点
轴时,点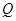 的坐标是
的坐标是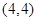 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)判断点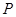 运动时,直线
运动时,直线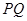 与椭圆
与椭圆 的公共点个数,并证明你的结论.
的公共点个数,并证明你的结论.
(本小题满分12分)如图,已知在直三棱柱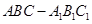 中,
中, 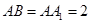 ,
,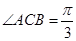 ,点D是线段
,点D是线段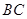 的中点.
的中点.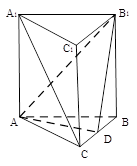
(Ⅰ)求证: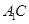 ∥平面
∥平面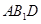 ;
;
(Ⅱ)当三棱柱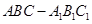 的体积最大时,求直线
的体积最大时,求直线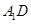 与平面
与平面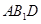 所成角
所成角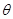 的正弦值.
的正弦值.
某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm).男队员身高在180cm以上定义为“高个子”,女队员身高在170cm以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.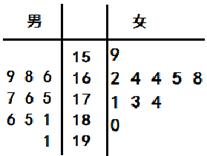
(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;
(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.
(本小题满分12分)已知函数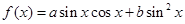 ,
,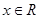 ,且
,且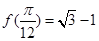 ,
,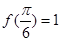 .
.
(Ⅰ)求函数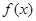 的单调递增区间;
的单调递增区间;
(Ⅱ)若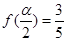 ,
,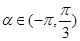 ,求
,求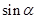 的值.
的值.
(本小题满分10分)选修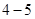 :不等式选讲
:不等式选讲
已知函数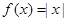 ,
,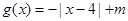
(Ⅰ)解关于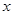 的不等式
的不等式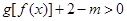 ;
;
(Ⅱ)若函数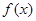 的图像恒在函数
的图像恒在函数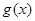 图像的上方,求实数
图像的上方,求实数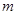 的取值范围.
的取值范围.