a11,a12,……a18
a21,a22,……a28
…………………
a81,a82,……a88
64个正数排成8行8列, 如上所示:在符合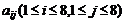 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且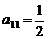 ,
,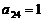 ,
, 。
。
⑴若 ,求
,求 和
和 的值。
的值。
⑵记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足 ,联
,联 (m为非零常数),
(m为非零常数), ,且
,且 ,求
,求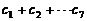 的取值范围。
的取值范围。
⑶对⑵中的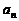 ,记
,记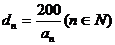 ,设
,设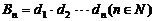 ,求数列
,求数列 中最大项的项数。
中最大项的项数。
已知函数 (其中
(其中 是自然对数的底数),
是自然对数的底数), ,
, .
.
(1)记函数 ,且
,且 ,求
,求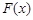 的单调增区间;
的单调增区间;
(2)若对任意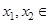
 ,
, ,均有
,均有 成立,求实数
成立,求实数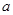 的取值范围.
的取值范围.
如图是一个半圆形湖面景点的平面示意图.已知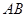 为直径,且
为直径,且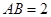 km,
km, 为圆心,
为圆心,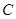 为圆周上靠近
为圆周上靠近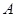 的一点,
的一点,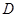 为圆周上靠近
为圆周上靠近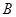 的一点,且
的一点,且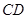 ∥
∥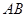 .现在准备从
.现在准备从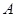 经过
经过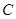 到
到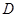 建造一条观光路线,其中
建造一条观光路线,其中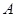 到
到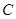 是圆弧
是圆弧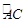 ,
,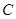 到
到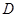 是线段
是线段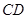 .设
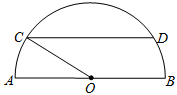
.设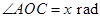 ,观光路线总长为
,观光路线总长为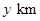 .
.
(1)求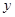 关于
关于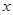 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
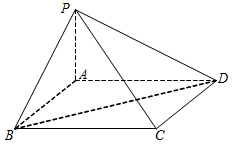
如图,在四棱锥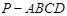 中,底面
中,底面 是菱形,且
是菱形,且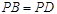 .
.
(1)求证: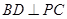 ;
;
(2)若平面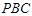 与平面
与平面 的交线为
的交线为 ,求证:
,求证: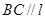 .
.
已知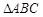 的内角
的内角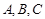 的对边分别为
的对边分别为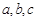 ,
,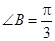 .
.
(1)若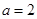 ,
,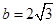 ,求
,求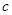 的值;
的值;
(2)若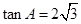 ,求
,求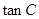 的值.
的值.
已知数列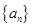 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有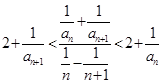 成立,且
成立,且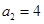 .
.
(1)求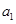 ,
, 的值;
的值;
(2)猜想数列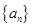 的通项公式,并给出证明.
的通项公式,并给出证明.