某商场今年销售计算机5000台.如果平均每年的销售量比上一年的销售量增加 ,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?
,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?
已知在等比数列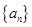 中,
中,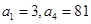 ,若数列
,若数列 满足:
满足: ,数列
,数列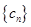 满足:
满足: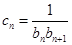 ,且数列
,且数列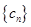 的前
的前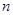 项和为
项和为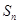 .
.
(1)求数列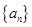 的通项公式;(2)求数列
的通项公式;(2)求数列 的通项公式; (3) 求
的通项公式; (3) 求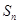 .
.
在△ 中,∠
中,∠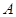 ,∠
,∠ ,∠
,∠ 的对边分别是
的对边分别是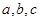 ,且
,且  .
.
(1)求∠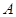 的大小;(2)若
的大小;(2)若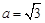 ,
, ,求
,求 和
和 的值.
的值.
已知函数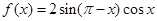 .
.
(1)求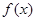 的最小正周期; (2)求
的最小正周期; (2)求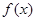 在区间
在区间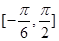 上的最大值和最小值.
上的最大值和最小值.
已知 ,
,
求 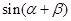 和
和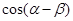 的值.
的值.
某港口的水深 (米)是时间
(米)是时间 (
( ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测,  可近似的看成是函数
可近似的看成是函数 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?