列{an}的前n项和为Sn,已知Sn+1=pSn+q(p,q为常数,n∈N*),a1=2,a2=1,a3=q-3p.
(1)求p,q的值;
(2)求数列{an}的通项公式;
(3)是否存在正整数m,n,使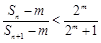 成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由.
成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由.
厂有215名工人接受了生产1000台GH型高科技产品的总任务,已知每台GH型产品由4个G型装置和3个H型装置配套组成.每个工人每小时能加工6个G型装置或2个H型装置.现将工人分成两组,每组分别加工一种装置.设加工G型装置的工人有x人,他们加工完G型装置所需时间为g(x),其余工人加工完H型装置所需时间为h(x)(单位:小时,可不为整数).
(1)写出g(x),h(x)的解析式;
(2)应怎样分组,才能使完成总任务时两组所需时间之和最少?
角坐标系中,已知向量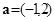 ,又点
,又点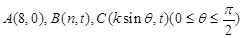
(1)若 且
且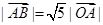 ,求向量
,求向量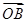 ;
;
(2)若向量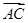 与向量
与向量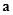 共线,当
共线,当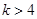 时,且
时,且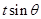 取最大值为4时,求
取最大值为4时,求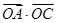
已知向量 ,
, ,函数
,函数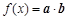 .
.
(1)求函数 定义域及最小正周期;
定义域及最小正周期;
(2)求函数 的单调减区间.
的单调减区间.
已知函数
 .
.
(1)求函数 的极值;
的极值;
(2)证明:当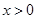 时,
时,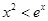 ;
;
(3)证明:对任意给定的正数 ,总存在
,总存在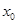 ,使得当
,使得当 ,恒有
,恒有 .
.