某市物价局调查了某种治疗H1N1流感的常规药品在2009年每个月的批发价格和该药品在药店的销售价格,调查发现,该药品的批发价格按月份以12元/盒为中心价随某一正弦曲线上下波动,且3月份的批发价格最高为14元/盒,7月份的批发价格最低为10元/盒。该药品在药店的销售价格按月份以14元/盒为中心价随另一正弦曲线上下波动,且5月份的销售价格最高为16元/盒,9月份的销售价格最低为12元/盒。
(Ⅰ)求该药品每盒的批发价格f(x)和销售价格g(x)关于月份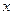 的函数解析式;
的函数解析式;
(Ⅱ)假设某药店每月初都购进这种药品p盒,且当月售完,求该药店在2009年哪些月份是盈利的?说明你的理由。
在一次模拟射击游戏中,小李连续射击了两次,设命题 :“第一次射击中靶”,命题
:“第一次射击中靶”,命题 :“第二次射击中靶”,试用
:“第二次射击中靶”,试用 ,
, 及逻辑连结词“或”“且”“非”表示下列命题:
及逻辑连结词“或”“且”“非”表示下列命题:
(1)两次射击均中靶; (2)两次射击均未中靶;

(3)两次射击恰好有一次中靶;(4)两次射击至少有一次中靶.
(本小题满分15分)已知函数,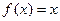 ,
,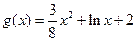 .
.
(Ⅰ)求函数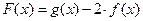 的极大值点与极小值点; (Ⅱ)若函数
的极大值点与极小值点; (Ⅱ)若函数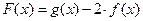 在
在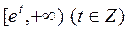 上有零点,求
上有零点,求 的最大值(
的最大值(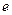 为自然对数的底数); (Ⅲ)设
为自然对数的底数); (Ⅲ)设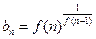 (
(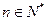 ),试问数列
),试问数列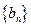 中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由.
(本小题满分14分)在平面直角坐标系中,O为坐标原点,已知向量 又点
又点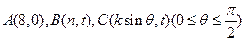 . (Ⅰ)若
. (Ⅰ)若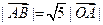 且
且 , 求向量
, 求向量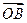 ; (Ⅱ)若向量
; (Ⅱ)若向量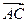 与向量
与向量 共线,当k
共线,当k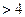 ,且
,且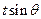 取最大值4时,求
取最大值4时,求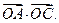
(本小题满分15分)已知数列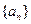 中,
中,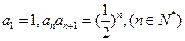 .
.
(Ⅰ)求证:数列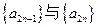 (
(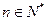 )均为等比数列; (Ⅱ)求数列
)均为等比数列; (Ⅱ)求数列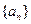 的前
的前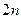 项和
项和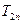 ; (Ⅲ)若数列
; (Ⅲ)若数列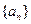 的前
的前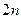 项和为
项和为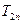 ,不等式
,不等式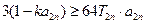 对
对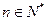 恒成立,求
恒成立,求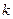 的最大值.
的最大值.
 (本小题满分14分)如下图,某小区准备绿化一块直径为
(本小题满分14分)如下图,某小区准备绿化一块直径为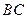 的半圆形空地,
的半圆形空地,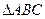 的内接正方形
的内接正方形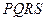 为一水池,
为一水池,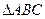 外的地方种草,其余地方种花.若
外的地方种草,其余地方种花.若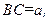
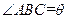 ,设
,设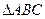 的面积为
的面积为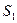 ,正方形
,正方形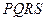 的面积为
的面积为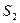 ,将比值
,将比值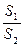 称为“规划合理度”. (Ⅰ)试用
称为“规划合理度”. (Ⅰ)试用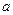 ,
,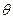 表示
表示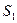 和
和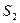 ; (Ⅱ)若
; (Ⅱ)若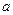 为定值,当
为定值,当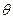 为何值时,“规划合理度”最小?并求出这个最小值.
为何值时,“规划合理度”最小?并求出这个最小值.