如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1,B1C1的中点.问:
(1)AM和CN是否是异面直线?说明理由;
(2)D1B和CC1是否是异面直线?说明理由.
(本小题满分10分)选修4-4:坐标系与参数方程
已知圆C的参数方程为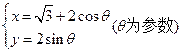 ,若P是圆C与y轴正半轴的交点,以圆心C为
,若P是圆C与y轴正半轴的交点,以圆心C为
极点,x轴的正半轴为极轴建立极坐标系,求过点P的圆C的切线的极坐标方程.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
如图,在直径是AB的半圆上有两个不同的点M、N,设AN与BM的交点是P.
求证: .
.
(本小题满分12分)
已知函数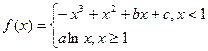
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是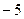 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求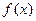 在区间
在区间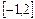 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线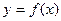 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得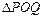 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由。
轴上?说明理由。
(本小题满分12分)
已知m>1,直线 ,椭圆C:
,椭圆C: ,
,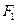 、
、 分别为椭圆C左、右焦点.
分别为椭圆C左、右焦点.
(Ⅰ)当直线过右焦点 时,求直线的方程;
时,求直线的方程;
(Ⅱ)设直线与椭圆C交于A、B两点,△A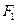
 、△B
、△B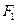
 的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
的重心分别为G、H.若原点O在以线段GH为直径的圆内,求实数m的取值范围.
(本小题满分12分)
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
(Ⅰ)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(Ⅱ)从频率分布直方图中,估计本次考试的平均分;
(Ⅲ)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.