如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
(1)求证:AB∥平面EFGH,CD∥平面EFGH.
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
已知函数f(x)=x3+Ax2﹣9x+1,下列结论中错误的是()
A. x0∈R,f(x0)=0 x0∈R,f(x0)=0 |
| B.“A=3”是“﹣3为f(x)的极大值点”的充分不必要条件 |
| C.若x0是f(x)的极小值点,则f(x)在区间(x0,+∞)单调递增 |
| D.若3是f(x)的极值点,则f(x)的单调递减区间是(﹣1,3) |
(本小题满分14分)已知函数f(x)=xln(1+x)-a(x+1),其中a为实常数.
(1)当x∈[1,+∞)时,f′(x)>0恒成立,求a的取值范围;
(2)求函数g(x)=f′(x)-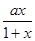 的单调区间.
的单调区间.
(本小题满分12分)四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC= ,
,
(1)求证:PD⊥平面ABCD;
(2)求证,直线PB与AC垂直;
(本小题满分12分)已知数列{ }是公差不为0的等差数列,a1=2且a2, a3, a4+1成等比数列.
}是公差不为0的等差数列,a1=2且a2, a3, a4+1成等比数列.
(1)求数列{ }的通项公式;
}的通项公式;
(2)设 ,求数列{
,求数列{ }的前n项和
}的前n项和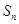
(本小题满分12分)若函数f(x)=ax2+2x- ln x在x=1处取得极值.
ln x在x=1处取得极值.
(1)求a的值;
(2)求函数f(x)的单调区间及极值.