如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8.BC是⊙O的直径,AB=AC=6,
OE∥AD.
(1)求二面角B-AD-F的大小;
(2)求直线BD与EF所成的角的余弦值.
已知 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))
(I) 若 ,求函数
,求函数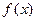 的单调递增区间;
的单调递增区间;
(II)若函数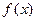 的导函数
的导函数 满足:当|x|≤1时,有|
满足:当|x|≤1时,有| |≤
|≤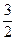 恒成立,求函数
恒成立,求函数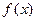 的解析表达式;
的解析表达式;
(III)若0<a<b, 函数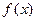 在
在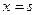 和
和 处取得极值,且
处取得极值,且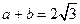 ,证明:
,证明: 与
与 不可能垂直.
不可能垂直.
已知二次函数 为常数);
为常数); .若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
.若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
(Ⅰ)求a、b、c的值;
(Ⅱ)求阴影面积S关于t的函数S(t)的解析式;
(Ⅲ)若 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
已知函数 ,函数
,函数 .
.
(1)当 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)设函数h(x)=(1-x)f(x)+16,试根据m的取值分析函数h(x)的图象与函数g(x)的图象交点的个数.
设函数
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈[a+1, a+2]时,不等 ,求a的取值范围.
,求a的取值范围.
已知函数f(x)=ax2+bx+c,其中a∈N*,b∈N,c∈Z。
(1)若b>2a,且f(sinx)(x∈R)的最大值为2,最小值为-4,试求函数f(x)的最小值;
(2)若对任意实数x,不等式4x≤f(x)≤2(x2+1)恒成立,且存在x0,使得f(x0)<2(x02+1)成立,求c的值。