如图所示,在三棱柱ABC—A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.
(1)求证:平面CA1B⊥平面A1ABB1;
(2)求直线A1C与平面BCC1B1所成角的正切值;
(3)求点C1到平面A1CB的距离.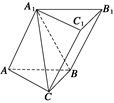
已知正三棱柱 的每条棱长均为
的每条棱长均为 ,
, 为棱
为棱 上的动点,
上的动点,
(1)当 在何处时,
在何处时, ∥平面
∥平面 ,并证明之;
,并证明之;
(2)在(1)下,求平面 与平面
与平面 所成锐二面角的正切值。
所成锐二面角的正切值。
美国篮球职业联赛( ),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
(1)组织者在此次决赛中获门票收入为1200万美元的概率是多少?
(2)组织者在此次决赛中获门票收入不低于1800万美元的概率是多少?
在三棱柱 ,已知
,已知 是正方形且边长为
是正方形且边长为 ,
, 为矩形,且平面
为矩形,且平面 ⊥平面
⊥平面

(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)求点 到平面
到平面 的距离。
的距离。
(本小题满分12分)已知函数 ,
, ,函数
,函数
在 、
、 处取得极值,其中
处取得极值,其中 。
。
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)判断 在
在 上的单调性;
上的单调性;
(Ⅲ)已知 在
在 上的最大值比最小值大
上的最大值比最小值大  ,若方程
,若方程 有3个不同的解,
有3个不同的解,
求实数 的取值范围。
的取值范围。
(本小题满分12分)如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, ⊥平面
⊥平面 ,
, ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。
(Ⅰ)证明: ⊥
⊥ ;
; (Ⅱ)若
(Ⅱ)若 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。