已知正三棱柱 的每条棱长均为
的每条棱长均为 ,
, 为棱
为棱 上的动点,
上的动点,
(1)当 在何处时,
在何处时, ∥平面
∥平面 ,并证明之;
,并证明之;
(2)在(1)下,求平面 与平面
与平面 所成锐二面角的正切值。
所成锐二面角的正切值。
.已知:圆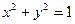 过椭圆
过椭圆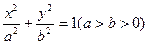 的两焦点,与椭圆有且仅有两个公共点:直线
的两焦点,与椭圆有且仅有两个公共点:直线 与圆
与圆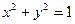 相切 ,与椭圆
相切 ,与椭圆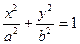 相交于A,B两点记
相交于A,B两点记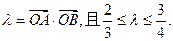
(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围;
的取值范围;
(Ⅲ)求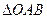 的面积S的取值范围.
的面积S的取值范围.
.如图1,直角 梯形ABCD中,
梯形ABCD中, ,
, E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.
E,F分别为边AD和BC上的点,且EF//AB,AD=2AE=2AB=4FC=4将四边形EFCD沿EF折起(如图2),使AD=AE.
(Ⅰ)求证:BC//平面DAE;
(Ⅱ)求四棱锥D—AEFB的体积;
(Ⅲ)求面CBD与面DAE所成锐二面角的余弦值.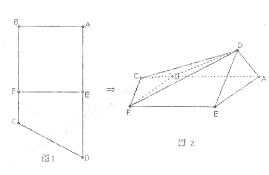
在数列 中,
中,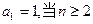 时,其前
时,其前 项和
项和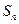 满足:
满足: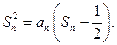
(Ⅰ)求 ;
;
(Ⅱ)令 ,求数列
,求数列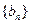 的前项和
的前项和
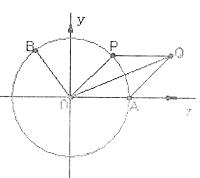
如图,A是单位圆与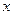 轴正半轴的交点,点B、P在单位圆上,且
轴正半轴的交点,点B、P在单位圆上,且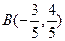 ,
,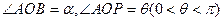 ,
,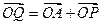 ,四边形OAQP的面积为S.
,四边形OAQP的面积为S.
(Ⅰ)求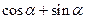 ;
;
(Ⅱ)求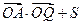 的最大值及此时
的最大值及此时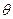 的值
的值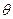 0.
0.
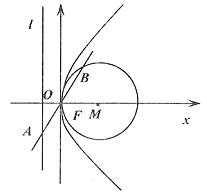
已知抛物线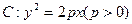 的准线为
的准线为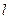 ,焦点为F,
,焦点为F, 的圆心在
的圆心在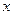 轴的正半轴上,且与
轴的正半轴上,且与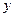 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为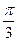 的直线
的直线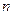 ,交
,交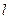 于点A,交
于点A,交 于另一点B,且AO=OB=2.
于另一点B,且AO=OB=2.
(1)求 和抛物线C的方程;
和抛物线C的方程;
(2)若P为抛物线C上的动点,求 的最小值;
的最小值;
(3)过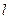 上的动点Q向
上的动点Q向 作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.