美国篮球职业联赛( ),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
),某赛季的总决赛在洛杉矶湖人队与费城76人队之间角逐,采用七局四胜制,即若有一队胜四场,由此队获胜且比赛结束,因两队实力水平非常接近,在每场比赛中两队获胜是等可能的,据以往资料统计,每场比赛组织者可获门票收入300万美元,两队决出胜负后问:
(1)组织者在此次决赛中获门票收入为1200万美元的概率是多少?
(2)组织者在此次决赛中获门票收入不低于1800万美元的概率是多少?
已知函数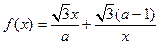 (
(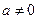 且
且 ).
).
(1) 试就实数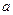 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当 时,函数在
时,函数在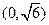 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求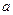 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线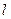 ,使得
,使得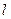 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出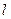 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
定义在区间(0, )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有 .
.
(1)求证:方程f(x)=0有且只有一个实根;
(2)若a>b>c>1,且a、b、c成等差数列,求证: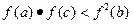 ;
;
(3)(本小题只理科做)若f(x) 单调递增,且m>n>0时,有 ,求证:
,求证: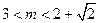
已知函数 在区间[0,1]上单调递增,在区间[1,2]上单调递减;
在区间[0,1]上单调递增,在区间[1,2]上单调递减;
(1)求a的值;
(2)求证:x=1是该函数的一条对称轴; (3)是否存在实数b,使函数
(3)是否存在实数b,使函数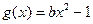 的图象与函数f(x)的图象恰好有两个交点?若存在,求出b的值;若不存在,请说明理由.
的图象与函数f(x)的图象恰好有两个交点?若存在,求出b的值;若不存在,请说明理由.
函数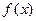 的定义域为R,并满足以下条件:①对任意
的定义域为R,并满足以下条件:①对任意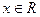 ,有
,有 ;
;
②对任意 、
、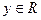 ,有
,有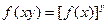 ;③
;③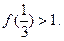 则
则
(1)求 的值;
的值;
(2)求证: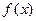 在R上是单调增函数;
在R上是单调增函数;
(3)若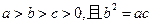 ,求证:
,求证:
已知函数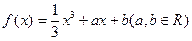 在
在 处取得的极小值是
处取得的极小值是 .
.
(1)求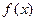 的单调递增区间;
的单调递增区间;
(2)若 时,有
时,有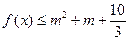 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.