一名学生每天骑车上学,从他家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 .
.
(1)设X为这名学生在途中遇到红灯的次数,求X的分布列;
(2)设Y为这名学生在首次停车前经过的路口数,求Y的概率分布;
(3)求这名学生在途中至少遇到一次红灯的概率.
某班同学寒假期间在三个小区进行了一次有关“年夜饭在哪吃”的调查,若年夜饭在家吃的称为“传统族”,否则称为“前卫族”,这两类家庭总数占各自小区家庭总数的比例如下:
| A小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
| B小区 |
传统族 |
前卫族 |
| 比例 |
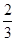 |
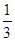 |
| C小区 |
传统族 |
前卫族 |
| 比例 |
 |
 |
(Ⅰ)从A , B , C三个小区中各选一个家庭,求恰好有2个家庭是“传统族”的概率(用比例作为相应的概率);
(Ⅱ)在C小区按上述比例选出的20户家庭中,任意抽取3户家庭,其中“前卫族”家庭的数量记为X,求X的分布列和期望 .
.
已知函数 (其中
(其中 ).
).
(Ⅰ)求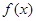 的单调区间;
的单调区间;
(Ⅱ)求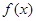 在
在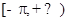 上的最大值与最小值.
上的最大值与最小值.
已知函数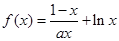 .
.
①若函数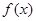 在
在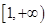 上是增函数,求正实数
上是增函数,求正实数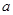 的取值范围;
的取值范围;
②若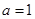 ,
,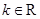 且
且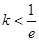 ,设
,设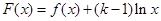 ,求函数
,求函数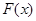 在
在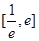 上的最大值和最小值。
上的最大值和最小值。
曲线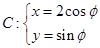 (
(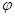 为参数),若点
为参数),若点 是曲线
是曲线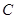 上的动点
上的动点
①求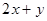 的取值范围
的取值范围
②求直线 被曲线C截得的弦长
被曲线C截得的弦长
某商场销售某种商品的经验表明,该商品每日的销售量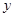 (单位:千克)与销售价格
(单位:千克)与销售价格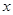 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
①求 的值;
的值;
②若该商品的成本为3元/千克, 试确定销售价格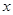 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.