设a,b,c为正实数.求证: +abc≥2
+abc≥2 .
.
把一颗骰子投掷2次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,试就方程组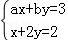 解答下列各题:
解答下列各题:
(1)求方程组只有一个解的概率;
(2)求方程组只有正数解的概率.
考取驾照是一个非常严格的过程,有的人并不能一次性通过,需要进行补考,现在有一张某驾校学员第一次考试结果汇总表: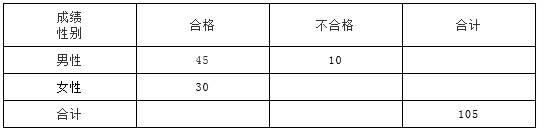
(1)完成列联表
(2)根据列联表判断性别与考试成绩是否有关系,如果有关系求出精确地可信度,没关系请说明理由.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
| x |
3 |
4 |
5 |
6 |
| t |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y= x+
x+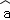 ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为92吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数据:3×2.5+4×3+5×4+6×4.5=66.5)
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]
(Ⅰ)求频率分布图中a的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)求出本次评分的众数、中位数、平均数.
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
| 品种甲 |
403 |
397 |
390 |
404 |
388 |
400 |
412 |
406 |
| 品种乙 |
419 |
403 |
412 |
418 |
408 |
423 |
400 |
413 |
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如表:分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?