课外活动小组共13人,其中男生8人,女生5人,并且男、女各指定一名队长,现从中选5人主持某种活动,依下列条件各有多少种选法?
(1)只有一名女生;
(2)两队长当选;
(3)至少有一名队长当选;
(4)至多有两名女生当选.
(本小题满分12分)已知椭圆 的右焦点为F,离心率为
的右焦点为F,离心率为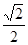 ,过点F且与x轴垂直的直线被椭圆截得的线段长为
,过点F且与x轴垂直的直线被椭圆截得的线段长为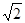 ,O为坐标原点.
,O为坐标原点.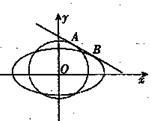
(Ⅰ)求椭圆C的方程
(Ⅱ)如图所示,设直线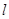 与圆
与圆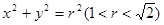 、椭圆C同时相切,切点分别为A,B,求|AB|的最大值.
、椭圆C同时相切,切点分别为A,B,求|AB|的最大值.
(本小题满分12分)在如图所示的空间几何体中,平面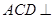 平面
平面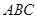 ,
,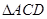 与
与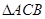 是边长为
是边长为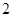 的等边三角形,
的等边三角形,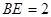 ,
,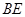 和平面
和平面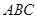 所成的角为
所成的角为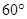 ,且点
,且点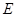 在平面
在平面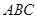 上的射影落在
上的射影落在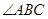 的平分线上.
的平分线上.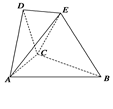
(1)求证: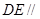 平面
平面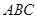 ;
;
(2)求二面角 的余弦值
的余弦值
(本小题满分1 2分)2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩。
为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(1)完成被调查人员的频率分布直方图;
(2)若年龄在[15,25),[55,65)的被调查者中赞成人数分别为4人和3人,现从这两组的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“改革方案”的人数为X,求随机变量X的分布列和数学期望.
(本小题满分12分)对于给定数列{an},如果存在实常数p,q,使得an+1=pan+q对于任意n∈N*都成立,我们称数列{an}是“M类数列”.
(1)已知数列{bn}是“M类数列”且bn= 3n求它对应的实常数p,q的值;
(2)若数列{cn}满足c1=-l,cn - cn+l =2n(n∈N*),求数列{cn}的通项公式.判断{cn}是否为“M类数列”并说明理由。
设函数f(x) =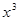 -6x+5,
-6x+5,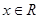 .
.
(1)求f(x)的极值;
(2)若关于x的方程 f(x) = a有3个不同实根,求实数a的取值范围;
(3)已知当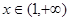 .时,f(x)
.时,f(x)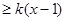 恒成立,求实数 k的取值范围
恒成立,求实数 k的取值范围