设三条直线l1:x+y-1=0,l2:kx-2y+3=0,l3:x-(k+1)y-5="0." 若这三条直线交于一点,求k的值.
(本小题满分12分)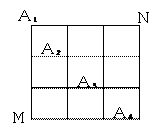
如图,在某城市中,M,N两地之间有整齐的方格形道路网,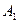 、
、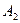 、
、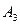 、
、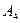 是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
(Ⅰ)求甲由M处到达N处的不同走法种数;
(Ⅱ)求甲经过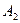 的概率.
的概率.
(本小题满分12分)
若某一等差数列的首项为 的常数项,其中m是
的常数项,其中m是 -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值.
(本小题满分12分)
已知盒子中有六张分别标有数字1、2、3、4、5、6的卡片
(Ⅰ)现从盒子中任取两张卡片,将卡片上的数字相加,求所得数字是奇数的概率;
(Ⅱ)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张标有数字为偶数的卡片则停止抽取,否则继续进行,求抽取次数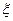 的分布列.
的分布列.
(本小题满分10分)
已知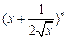 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(Ⅰ)求n的值;
(Ⅱ)求展开式中系数最大的项.
(本小题满分12分)
|
如图,把边长为a的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;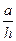 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?