角 终边上的点P与A(a,2a)关于x轴对称(a≠0),角
终边上的点P与A(a,2a)关于x轴对称(a≠0),角 终边上的点Q与A关于直线y=x对称,求sin
终边上的点Q与A关于直线y=x对称,求sin ·cos
·cos +sin
+sin ·cos
·cos +tan
+tan ·tan
·tan 的值.
的值.
已知点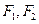 是双曲线M:
是双曲线M: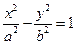 的左右焦点,其渐近线为
的左右焦点,其渐近线为 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线M的方程;
(2) 过 的直线
的直线 与M相交于
与M相交于 、
、 两点,直线
两点,直线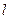 的法向量为
的法向量为 ,且
,且 ,求k的值;
,求k的值;
(3)在(2)的条件下,若双曲线M在第四象限的部分存在一点C满足 ,求m的值及△ABC的面积
,求m的值及△ABC的面积 .
.
已知函数 (k为常数),
(k为常数), 是函数
是函数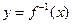 图像上的点.
图像上的点.
(1)求实数k的值及函数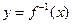 的解析式;
的解析式;
(2)将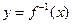 的图像按向量
的图像按向量 平移得到函数y=g(x)的图像.
平移得到函数y=g(x)的图像.
若 对任意的
对任意的 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
已知函数 .
.
(1)将f(x)写成 (
(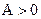 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;
(2)如果△ABC的三边a、b、c满足 ,且边b所对的角为x,试求x的取值范围及此时函数f(x)的值域.
,且边b所对的角为x,试求x的取值范围及此时函数f(x)的值域.
已知函数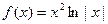 ,
,
(Ⅰ)判断函数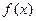 的奇偶性;
的奇偶性;
(Ⅱ)求函数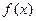 的单调区间;
的单调区间;
(Ⅲ)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围.
的取值范围.
已知数列 满足:
满足: ,且对任意
,且对任意 N*都有
N*都有 .
.
(Ⅰ)求 ,
, 的值;
的值;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)证明: =
= (
( N*).
N*).