(1)已知扇形的周长为10,面积为4,求扇形中心角的弧度数;
(2)已知扇形的周长为40,当它的半径和中心角取何值时,才能使扇形的面积最大?最大面积是多少?
已知函数 的图象分别与
的图象分别与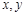 轴相交于两点
轴相交于两点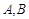 ,且向量
,且向量 (
(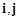 分别是与
分别是与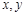 轴正半轴同方向的单位向量),又函数
轴正半轴同方向的单位向量),又函数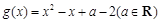 .
.
(1)求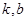 的值;
的值;
(2)若不等式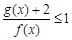 的解集为
的解集为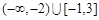 ,求
,求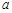 的值
的值
已知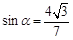 ,
,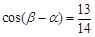 ,且
,且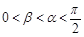 .
.
(1)求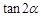 的值;
的值;
(2)求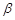 的值.
的值.
如图所示,F1、F2分别为椭圆C: 的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为
的左、右两个焦点,A、B为两个顶点,该椭圆的离心率为 ,
, 的面积为
的面积为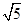 .
.
(1)求椭圆C的方程和焦点坐标;
(2)作与AB平行的直线 交椭圆于P、Q两点,
交椭圆于P、Q两点,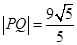 ,求直线
,求直线 的方程.
的方程.
设函数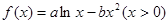 ,若函数
,若函数 在
在 处与直线
处与直线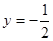 相切,
相切,
(1)求实数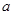 ,
,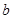 的值;(2)求函数
的值;(2)求函数 上的最大值.
上的最大值.
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本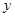 (万元)可以看成月产量
(万元)可以看成月产量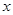 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本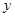 (万元)关于月产量
(万元)关于月产量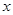 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?