已知函数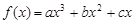 的导函数为
的导函数为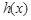 ,
,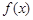 的图象在点
的图象在点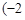 ,
,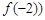 处的切线方程为
处的切线方程为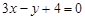 ,且
,且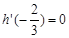 ,直线
,直线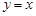 是函数
是函数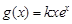 的图象的一条切线.
的图象的一条切线.
(1)求函数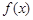 的解析式及
的解析式及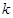 的值;
的值;
(2)若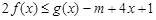 对于任意
对于任意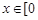 ,
,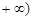 恒成立,求实数
恒成立,求实数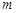 的取值范围.
的取值范围.
(Ⅰ)求右焦点坐标是(2,0),且经过点 的椭圆的标准方程
的椭圆的标准方程
(Ⅱ)求与椭圆 共焦点且过点
共焦点且过点 的双曲线的标准方程.
的双曲线的标准方程.
已知函数 是偶函数.
是偶函数.
(1)求k的值;
(2)若函数y=f(x)的图象与直线 没有交点,求b的取值范围.
没有交点,求b的取值范围.
(3)设 ,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
若函数f(x)=logax(0<a<1)在区间[2,8]上的最大值与最小值之差为2,求a的值.
已知函数f(x)=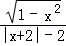 .
.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并说明理由.