(本小题满分12分)某项计算机考试按科目A、科目B依次进行,只有大拿感科目A成绩合格时,才可继续参加科目B的考试,已知每个科目只允许有一次补考机会,两个科目均合格方快获得证书,现某人参加这项考试,科目A每次考试成绩合格的概率为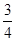 ,科目B每次考试合格的概率为
,科目B每次考试合格的概率为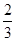 ,假设各次考试合格与否均互不影响.
,假设各次考试合格与否均互不影响.
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这次考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为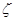 ,求随即变量
,求随即变量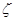 的分布列和数学期望.
的分布列和数学期望.
(本小题满分l2分) 如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.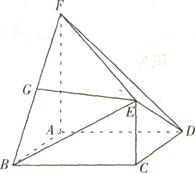
(I)求证:EG 面ABF;
面ABF;
(Ⅱ)若AF=AB,求二面角B—EF—D的余弦值.
(本小题满分l0分) 在等比数列 中,已知
中,已知 .
. 求数列
求数列 的通项公式;
的通项公式; 设数列
设数列 的前n项和为
的前n项和为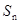 ,求
,求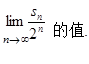
已知函数f(x)=lnx+
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设m R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
(Ⅲ)证明:ln2 l+ 1n22,+…+ln2 n> ∈N*).
∈N*).
设点P是圆x2 +y2 =4上任意一点,由点P向x轴作垂线PP0,垂足为Po,且 .
.
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设直线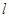 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
(1)若直线OA,AB,OB的斜率成等比数列,求实数m的取值范围;
(2)若以AB为直径的圆过曲线C与x轴正半轴的交点Q,求证:直线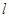 过定点(Q点除外),并求出该定点的坐标.
过定点(Q点除外),并求出该定点的坐标.