六个面分别写上1,2,3,4,5,6的正方体叫做骰子。问
1) 共有多少种不同的骰子;
2) 骰子相邻两个面上数字之差的绝对值叫做这两个面之间的变差,变差的总和叫做全变差V。在所有的骰子中,求V的最大值和最小值。
如图,从边长为 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为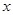 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度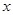 与底面正方形的边长的比不超过常数
与底面正方形的边长的比不超过常数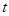 ,问:
,问: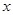 取何值时,长方体的容积V有最大值?
取何值时,长方体的容积V有最大值?
如图,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥
平面ABCD, SA=AB=BC=2,AD=1.
(Ⅰ)求SC与平面ASD所成的角余弦;
(Ⅱ)求平面SAB和平面SCD所成角的余弦.
已知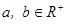 ,试证:
,试证: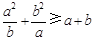 ;并求函数
;并求函数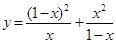 (
( )的最小值.
)的最小值.
已知 :
:
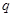 :
: .
.
(Ⅰ)若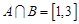 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 是
是 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.
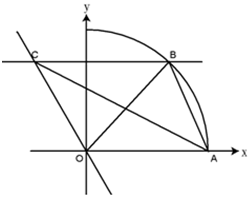
(本小题满分14分)在如图所示的直角坐标系中, 为单位圆在第一象限内圆弧上的动点,
为单位圆在第一象限内圆弧上的动点,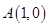 ,设
,设 ,过
,过 作直线
作直线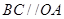 ,并交直线
,并交直线 于点
于点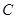 .
.
(Ⅰ)求点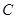 的坐标 (用
的坐标 (用 表示) ;
表示) ;
(Ⅱ)判断 能否为
能否为 ?若能,求出点
?若能,求出点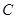 的坐标,若不能,请说明理由.
的坐标,若不能,请说明理由.
(Ⅲ) 试求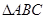 的面积的最大值,并求出相应
的面积的最大值,并求出相应 值.
值.