已知
过定点
，圆心
在抛物线
：
上运动，
为圆在
轴上所截得的弦．
⑴当点运动时，
是否有变化？并证明你的结论；
⑵当
是
与
的等差中项时，
试判断抛物线的准线与圆的位置关系，
并说明理由。
已知△ABC的三个内角A、B、C满足A+C=2B.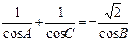
，求cos
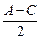的值.
已知△ABC的三内角A、B、C满足A+C=2B，设x=cos
，f(x)=cosB(
).
(1)试求函数f(x)的解析式及其定义域；
(2)判断其单调性，并加以证明；
(3)求这个函数的值域.
在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北30°东，俯角为30°的B处，到11时10分又测得该船在岛北60°西、俯角为60°的C处。
(1)求船的航行速度是每小时多少千米；
(2)又经过一段时间后，船到达海岛的正西方向的D处，问此时船距岛A有多远？
已知函数f(x)=2cosxsin(x+
)－
sin2x+sinxcosx
(1)求函数f(x)的最小正周期；
(2)求f(x)的最小值及取得最小值时相应的x的值；
(3)若当x∈［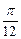
，
］时，f(x)的反函数为f－1(x)，求f-－1(1)的值。
设关于x的函数y=2cos2x－2acosx－(2a+1)的最小值为f(a)，试确定满足f(a)=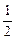
的a值，并对此时的a值求y的最大值.