已知点A(2,8),B(x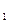 ,y
,y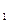 ),C(x
),C(x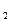 ,y
,y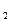 )在抛物线y
)在抛物线y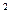 =2px上,△ABC的重心与此抛物线的焦点F重合(如图)。
=2px上,△ABC的重心与此抛物线的焦点F重合(如图)。
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标。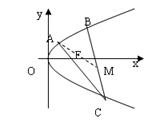
小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30o,小丽向前走了10米到达点E,此时的仰角为60o,求旗杆的高度。
已知 ,求代数式
,求代数式 的值.
的值.
解不等式: ,并把解集表示在数轴上.
,并把解集表示在数轴上.
已知:线段 ,直线
,直线 外一点A.求作:Rt△ABC,使直角边为AC(AC⊥
外一点A.求作:Rt△ABC,使直角边为AC(AC⊥ ,垂足为C)斜边AB=c.
,垂足为C)斜边AB=c.
大学生小刘回乡创办小微企业,初期购得原材料若干吨,每天生产相同件数的某种产品,单件产品所耗费的原材料相同.当生产6天后剩余原材料36吨,当生产10天后剩余原材料30吨.若剩余原材料数量小于或等于3吨,则需补充原材料以保证正常生产.
(1)求初期购得的原材料吨数与每天所耗费的原材料吨数;
(2)若生产16天后,根据市场需求每天产量提高20%,则最多再生产多少天后必须补充原材料?