.(本小题满分14分)已知直线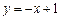 与椭圆
与椭圆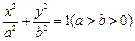 相交于
相交于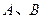 两点,且
两点,且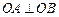 (其中
(其中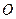 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为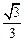 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)求证:不论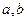 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点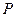
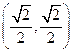 ;
;
(3)若直线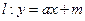 过(2)中的定点
过(2)中的定点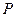 ,且椭圆的离心率
,且椭圆的离心率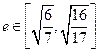 ,求原点到直线
,求原点到直线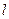 距离的取值范围.
距离的取值范围.
数列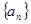 的各项均为正数,
的各项均为正数,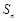 为其前
为其前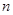 项和,对于任意
项和,对于任意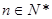 ,总有
,总有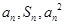 成等差数列.
成等差数列.
(Ⅰ)求数列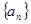 的通项公式;
的通项公式;
(Ⅱ)设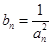 ,数列
,数列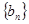 的前
的前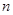 项和为
项和为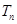 ,求证:
,求证: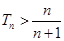 .
.
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,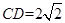 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点.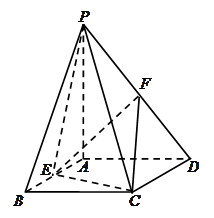
(Ⅰ)求证:平面PCE 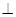 平面PCD;
平面PCD;
(Ⅱ)求四面体PEFC的体积.
甲、乙两个盒子里各放有标号为1,2,3,4的四个大小形状完全相同的小球,从甲盒中任取一小球,记下号码 后放入乙盒,再从乙盒中任取一小球,记下号码
后放入乙盒,再从乙盒中任取一小球,记下号码 .
.
(Ⅰ)求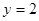 的概率;
的概率;
(Ⅱ)设随机变量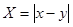 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
已知函数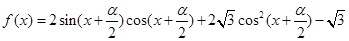 为偶函数, 且
为偶函数, 且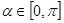
(Ⅰ)求 的值;
的值;
(Ⅱ)若 为三角形
为三角形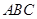 的一个内角,求满足
的一个内角,求满足 的
的 的值.
的值.
(本小题满分13分)
已知椭圆
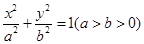 的离心率为
的离心率为 ,椭圆短轴长为
,椭圆短轴长为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知动直线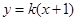 与椭圆
与椭圆 相交于
相交于 、
、 两点. ①若线段
两点. ①若线段 中点的横坐标为
中点的横坐标为 ,求斜率
,求斜率 的值;②若点
的值;②若点 ,求证:
,求证: 为定值。
为定值。