某市近10年的煤气消耗量与使用煤气户数的历史资料如下：
| 年 份 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
2002 |
| x用户（万户） |
1 |
1.2 |
1.6 |
1.8 |
2 |
2.5 |
3.2 |
4 |
4.2 |
4.5 |
| y （百万立米） |
6 |
7 |
9.8 |
12 |
12.1 |
14.5 |
20 |
24 |
25.4 |
27.5 |
（1）检验是否线性相关；（2）求回归方程；
（3）若市政府下一步再扩大5千煤气用户，试预测该市煤气消耗量将达到多少.
已知平面上的动点P（x，y）及两个定点A（-2，0），B（2，0），直线PA，PB的斜率分别为K1，K2且K1K2=－
(1).求动点P的轨迹C方程；
(2).设直线L：y=kx+m与曲线C交于不同两点，M，N，当OM⊥ON时，求O点到直线L的距离（O为坐标原点）
如图,E是以AB为直径的半圆弧上异于A，B的点，矩形ABCD所在平面垂直于该半圆所在的平面，且AB=2AD=2。
(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证：EF//AB；
②若EF=1，求三棱锥E—ADF的体积
已知向量
,设函数
.
(1).求函数f(x)的最小正周期;
(2).已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1,
，且
恰是函数f(x)在
上的最大值,求A,b和三角形ABC的面积.
设数列
是等差数列,且
且
成等比数列。
(1).求数列的通项公式
(2).设
，求前n项和
.
已知f(x)=|x+1|+|x-1|,不等式f(x)的解集为M.
(1)求M;
(2)当a,b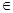
M时,证明:2|a+b|＜|4+ab|.